「3次元の内積の幾何学的な性質」の版間の差分
(→2次元の回転と2次元の内積) |
|||
| (1人の利用者による、間の19版が非表示) | |||
| 1行: | 1行: | ||
[[Category:数学]][[Category:線形代数]][[category:回転]] | [[Category:数学]][[Category:線形代数]][[category:回転]] | ||
| − | [[メインページ]]>[[数学の部屋 | + | [[メインページ]]>[[数学の部屋#回転]] |
==3次元の内積== | ==3次元の内積== | ||
| 16行: | 16行: | ||
3次元の内積は、2次元の内積の自然の拡張で、2つのベクトル <math>{\boldsymbol a}, {\boldsymbol b}</math> のデカルト座標での成分表示を | 3次元の内積は、2次元の内積の自然の拡張で、2つのベクトル <math>{\boldsymbol a}, {\boldsymbol b}</math> のデカルト座標での成分表示を | ||
<math>{\boldsymbol a} = (a_1, a_2, a_3), {\boldsymbol b} = (b_1, b_2, b_3)</math> とすると | <math>{\boldsymbol a} = (a_1, a_2, a_3), {\boldsymbol b} = (b_1, b_2, b_3)</math> とすると | ||
| + | |||
{{eqn|<math> | {{eqn|<math> | ||
{\boldsymbol a}\cdot{\boldsymbol b} = a_1b_1+a_2b_2+a_3b_3 | {\boldsymbol a}\cdot{\boldsymbol b} = a_1b_1+a_2b_2+a_3b_3 | ||
</math>|1}} | </math>|1}} | ||
| + | |||
と定義されますが、 | と定義されますが、 | ||
ベクトル <math>{\boldsymbol a}</math>、 <math>{\boldsymbol b}</math>それぞれ長さを <math>r_a</math>、<math>r_b</math> 、2つのベクトルのなす角度を <math>\beta </math> とすると、2次元の内積の結果をそのまま拡張すれば | ベクトル <math>{\boldsymbol a}</math>、 <math>{\boldsymbol b}</math>それぞれ長さを <math>r_a</math>、<math>r_b</math> 、2つのベクトルのなす角度を <math>\beta </math> とすると、2次元の内積の結果をそのまま拡張すれば | ||
| + | |||
{{eqn|<math> | {{eqn|<math> | ||
{\boldsymbol a}\cdot{\boldsymbol b} = a_1b_1+a_2b_2+a_3b_3 = r_ar_b\cos\beta | {\boldsymbol a}\cdot{\boldsymbol b} = a_1b_1+a_2b_2+a_3b_3 = r_ar_b\cos\beta | ||
</math>|2}} | </math>|2}} | ||
| + | |||
となりそうです。事実そうなるのですが、本当でしょうか? 証明してみましょう。 | となりそうです。事実そうなるのですが、本当でしょうか? 証明してみましょう。 | ||
| 61行: | 65行: | ||
| − | {{eqn|<math> | + | {{eqn|<math>\begin{align} |
| − | \begin{align} | + | {\boldsymbol a'}\cdot{\boldsymbol b'} &= |
| − | {\boldsymbol a'}\cdot{\boldsymbol b'} | + | (a_1\cos\beta-a_2\sin\beta)(b_1\cos\beta-b_2\sin\beta)+ \\ |
| − | &= (a_1\cos\beta-a_2\sin\beta) | + | &(a_1\sin\beta+a_2\cos\beta)(b_1\sin\beta+b_2\cos\beta) \\ &= |
| − | (b_1\cos\beta-b_2\sin\beta)+ | + | a_1b_1+a_2b_2\end{align}</math>|6}} |
| − | (a_1\sin\beta+a_2\cos\beta) | + | |
| − | (b_1\sin\beta+b_2\cos\beta) | + | |
| − | &=a_1b_1+a_2b_2 | + | |
| − | \end{align}</math>|6}} | + | |
| 88行: | 88行: | ||
| − | {{eqn|<math>\begin{align}{\boldsymbol a'} - {\boldsymbol b'}|^2 &= ({\boldsymbol a'}-{\boldsymbol b'})({\boldsymbol a'}-{\boldsymbol b'}) = {\boldsymbol a'}^2 + {\boldsymbol b'}^2 - 2{\boldsymbol a'}\cdot{\boldsymbol b'} \\ &= {\boldsymbol a}^2 + {\boldsymbol b}^2 - 2{\boldsymbol a}\cdot{\boldsymbol b}\end{align}</math>|8}} | + | {{eqn|<math>\begin{align}|{\boldsymbol a'} - {\boldsymbol b'}|^2 &= ({\boldsymbol a'}-{\boldsymbol b'})({\boldsymbol a'}-{\boldsymbol b'}) = {\boldsymbol a'}^2 + {\boldsymbol b'}^2 - 2{\boldsymbol a'}\cdot{\boldsymbol b'} \\ &= {\boldsymbol a}^2 + {\boldsymbol b}^2 - 2{\boldsymbol a}\cdot{\boldsymbol b}\end{align}</math>|8}} |
| 166行: | 166行: | ||
\right)</math> の内積は | \right)</math> の内積は | ||
| − | <math>{\boldsymbol a'}\cdot {\boldsymbol b'}=a'_1b'_1+a'_2b'_2+a'_3b'_3 | + | {{eqn|<math>{\boldsymbol a'}\cdot {\boldsymbol b'}=a'_1b'_1+a'_2b'_2+a'_3b'_3</math>|11}} |
| 175行: | 175行: | ||
同様に、<math>x</math>軸を回転軸とし、<math>x</math>軸の正方向に対して右回転する回転変換は | 同様に、<math>x</math>軸を回転軸とし、<math>x</math>軸の正方向に対して右回転する回転変換は | ||
| − | <math> | + | {{eqn|<math> |
\left(\begin{array}{ccc} | \left(\begin{array}{ccc} | ||
x' \\ | x' \\ | ||
| 196行: | 196行: | ||
z | z | ||
\end{array} \right) | \end{array} \right) | ||
| − | + | </math>|12}} | |
| − | + | ||
| − | </math> | + | |
<math>y</math>軸を回転軸とし、<math>y</math>軸の正方向に対して右回転する回転変換は | <math>y</math>軸を回転軸とし、<math>y</math>軸の正方向に対して右回転する回転変換は | ||
| − | <math> | + | {{eqn|<math> |
\left(\begin{array}{ccc} | \left(\begin{array}{ccc} | ||
x' \\ | x' \\ | ||
| 223行: | 221行: | ||
z | z | ||
\end{array} \right) | \end{array} \right) | ||
| − | + | </math>|13}} | |
| − | + | ||
| − | + | ||
| − | </math> | + | |
となります。いずれの回転も内積を変化させないのはいうまでもないでしょう。 | となります。いずれの回転も内積を変化させないのはいうまでもないでしょう。 | ||
| 252行: | 247行: | ||
*3次元の3軸による回転は内積を変更しない。つまり、2次元回転の場合と同様、図形を合同に変換し、辺の長さや辺のなす角度を変更しない。 | *3次元の3軸による回転は内積を変更しない。つまり、2次元回転の場合と同様、図形を合同に変換し、辺の長さや辺のなす角度を変更しない。 | ||
| − | 従って、2次元の内積の幾何学的な性質はそのまま3次元の内積でも成り立ち、ベクトル<math>{\boldsymbol a} | + | 従って、2次元の内積の幾何学的な性質はそのまま3次元の内積でも成り立ち、ベクトル<math>{\boldsymbol a},{\boldsymbol b}</math>の長さを <math>r_a</math>、<math>r_b</math>、ベクトル<math>{\boldsymbol a},{\boldsymbol b}</math> 同士のなす角度を <math>\beta</math> とすると |
| − | <math>{\boldsymbol a}\cdot{\boldsymbol b} = r_ar_b\cos\beta | + | {{eqn|<math>{\boldsymbol a}\cdot{\boldsymbol b} = r_ar_b\cos\beta</math>|14}} |
が成立します。以上で2次元の内積は3次元へ自然な形で拡張できることを示しました。 | が成立します。以上で2次元の内積は3次元へ自然な形で拡張できることを示しました。 | ||
2015年8月5日 (水) 05:24時点における最新版
3次元の内積
2次元の内積の幾何学的な性質では内積と2つのベクトルがなす角度との関係を紹介しました。この性質は実は3次元でもまったく同じなのですが、 3次元になるとこのことを説明するのが格段に難しくなります。
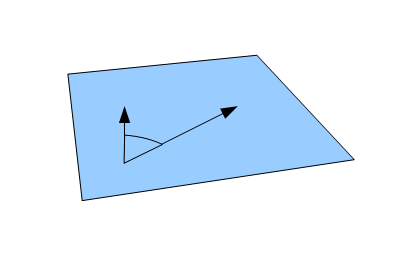
そもそも3次元で二つのベクトルのなす角度とはなんなのでしょうか?
図のように2つのベクトルの始点を同じ点として重ねると、2つのベクトルが同じ向きではなければ、2つのベクトルを含む 平面が決まります。2つのベクトルなす角度とは、この平面上での、つまり2次元での角度と同じものと考えることができます。
3次元の内積は、2次元の内積の自然の拡張で、2つのベクトル 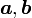 のデカルト座標での成分表示を
のデカルト座標での成分表示を
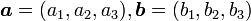 とすると
とすると
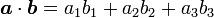
|
( 1 ) |
と定義されますが、
ベクトル 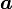 、
、 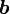 それぞれ長さを
それぞれ長さを 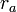 、
、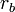 、2つのベクトルのなす角度を
、2つのベクトルのなす角度を 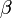 とすると、2次元の内積の結果をそのまま拡張すれば
とすると、2次元の内積の結果をそのまま拡張すれば
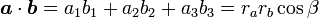
|
( 2 ) |
となりそうです。事実そうなるのですが、本当でしょうか? 証明してみましょう。
基本的には流れは以下の通り
- 2次元3次元の回転で内積が変化しないことを示す。
- 回転で2つベクトルを含む平面を x-y 平面に変換できることを示す。
- 内積が変化しないことの意味を示し、2次元の内積の性質がそのまま3次元でも成り立つことを示す。
2次元の回転と2次元の内積
まず、2次元に限定して、回転で内積が変化しないことを示しましょう。
ふたつの位置ベクトルを 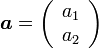 ,
,
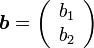 とすると、内積は
とすると、内積は
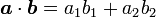
|
( 3 ) |
回転行列と複素数の積で示しましたように、位置ベクトルは回転行列をかけることで回転させることができます。
回転行列 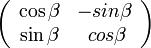 で、ベクトル
で、ベクトル 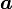 と
と 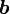 を回転させると、回転後のベクトル
を回転させると、回転後のベクトル 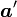 と
と 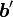 は
は
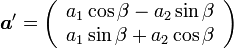
|
( 4 ) |
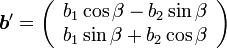
|
( 5 ) |
回転後の内積を計算すると
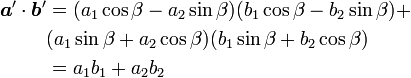
|
( 6 ) |
以上から、回転変換によって、内積が変化しないことがわかります。
内積が変化しないとはどういうことでしょうか?
ベクトルの大きさの2乗は 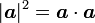 ですから、回転によって、ベクトルの大きさは変わりません。
ですから、回転によって、ベクトルの大きさは変わりません。
2個の位置ベクトル間の終点間距離の2乗は
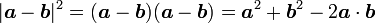
|
( 7 ) |
回転後の2個の位置ベクトル間の終点間距離の2乗は
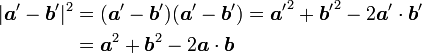
|
( 8 ) |
つまり、ベクトルの長さは回転によって変わりません。つまり、回転はベクトルが作る三角形を合同な三角形に変換します。従って、回転変換はベクトルがなす角度を変更しません。
3次元の回転
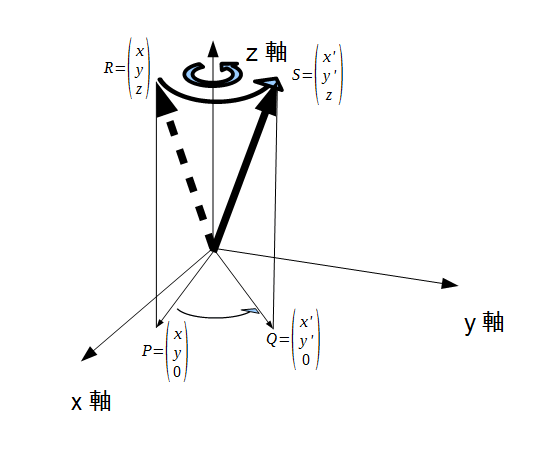
3次元の回転は意外と奥が深いので、ここでは x軸、y軸、z軸 を回転軸にした回転のみを扱います。
まず、z軸を回転軸にした3次元回転を考えてみましょう。
ここで z軸を回転軸とした回転とは、z軸の正方向に対して、図のように右回転する方向を正の角度の回転とします。
この回転は、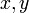 に関しては2次元の回転と同じになり、回転変換によって
に関しては2次元の回転と同じになり、回転変換によって 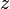 は変化しないので、変換行列は
は変化しないので、変換行列は
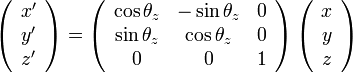
|
( 9 ) |
になります。
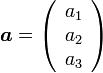 と
と
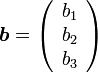 の3次元の内積は、2次元からの自然な拡張から
の3次元の内積は、2次元からの自然な拡張から
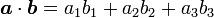
|
( 10 ) |
と定義しますが、
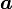 と
と 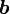 の回転後のベクトル
の回転後のベクトル 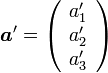 と
と
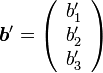 の内積は
の内積は
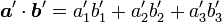
|
( 11 ) |
となります。このうち 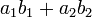 と
と 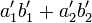 の部分は2次元の回転と同じなので同じになります。
の部分は2次元の回転と同じなので同じになります。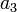 と
と 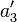 、
、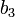 と
と 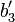 は同じなので、
は同じなので、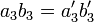 となります。
となります。
結局 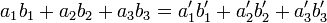 なので、
なので、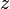 軸を回転軸とする回転変換で、内積は変化しないことになります。
軸を回転軸とする回転変換で、内積は変化しないことになります。
同様に、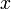 軸を回転軸とし、
軸を回転軸とし、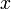 軸の正方向に対して右回転する回転変換は
軸の正方向に対して右回転する回転変換は
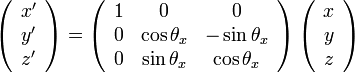
|
( 12 ) |
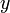 軸を回転軸とし、
軸を回転軸とし、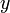 軸の正方向に対して右回転する回転変換は
軸の正方向に対して右回転する回転変換は
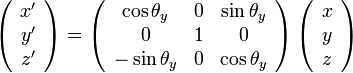
|
( 13 ) |
となります。いずれの回転も内積を変化させないのはいうまでもないでしょう。
3次元の内積
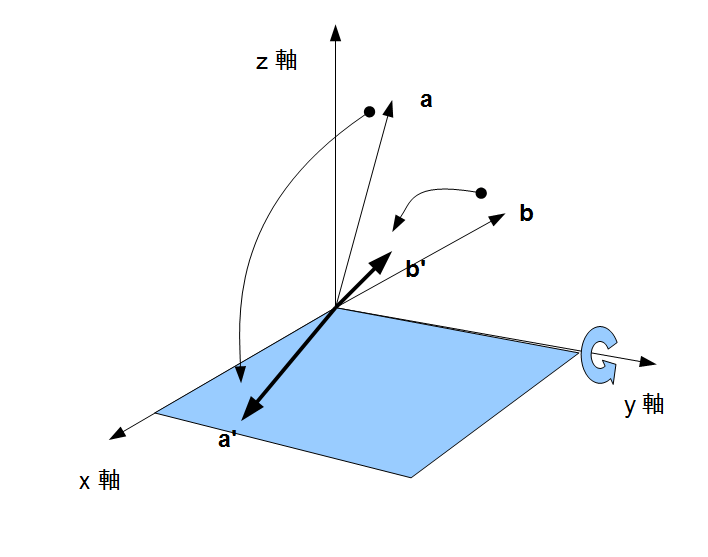
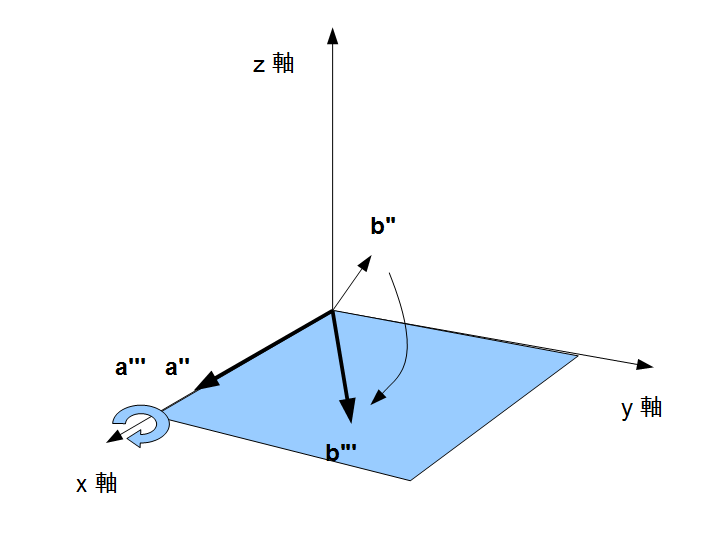
ここで、任意の2ベクトルを、内積を保ったまま、 平面内に回転変換できることを示します。まず下図のように、ベクトル
平面内に回転変換できることを示します。まず下図のように、ベクトル ,
, 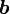 を
を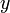 軸で回転させます。ベクトル
軸で回転させます。ベクトル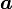 が
が 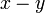 平面上にくるように回転させます。これを ベクトル
平面上にくるように回転させます。これを ベクトル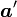 ,
, 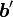 とします。
とします。
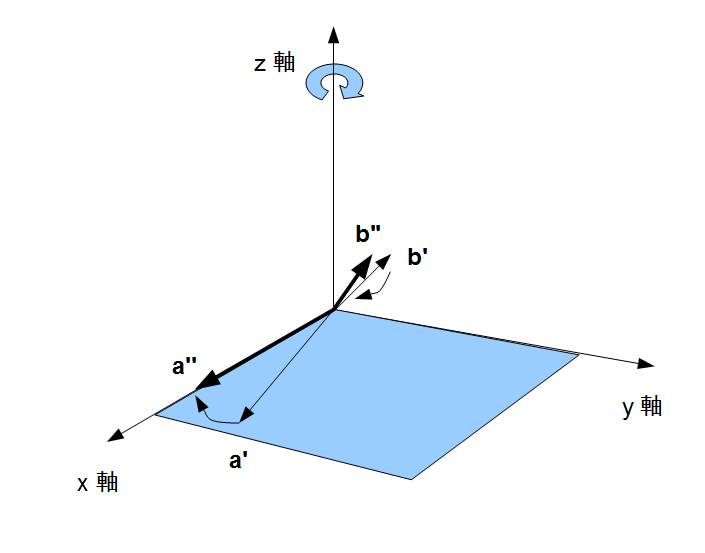
次に、ベクトル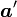 ,
, 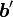
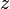 軸で回転させて、ベクトル
軸で回転させて、ベクトル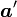 の方向を
の方向を 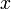 軸と一致させます。これを ベクトル
軸と一致させます。これを ベクトル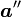 ,
, 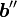 とします。
とします。
最後に, 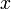 軸で回転変換を行って、
軸で回転変換を行って、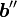 も
も 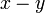 平面上に持ってきます。
平面上に持ってきます。
以上から
- 上のように3軸の回転変換で、任意の2ベクトルを
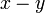 平面上に3次元の内積を変化させずにもってくることが出来る。
平面上に3次元の内積を変化させずにもってくることが出来る。
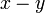 平面に移動したベクトルはz座標が0なので、3次元の内積は2次元の内積と一致する。
平面に移動したベクトルはz座標が0なので、3次元の内積は2次元の内積と一致する。
- 3次元の3軸による回転は内積を変更しない。つまり、2次元回転の場合と同様、図形を合同に変換し、辺の長さや辺のなす角度を変更しない。
従って、2次元の内積の幾何学的な性質はそのまま3次元の内積でも成り立ち、ベクトル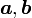 の長さを
の長さを 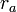 、
、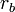 、ベクトル
、ベクトル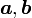 同士のなす角度を
同士のなす角度を 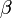 とすると
とすると
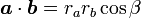
|
( 14 ) |
が成立します。以上で2次元の内積は3次元へ自然な形で拡張できることを示しました。