「複素数の乗算と除算の魔法」の版間の差分
提供: tknotebook
(→複素数の積と商) |
(→角度の加法定理) |
||
| (1人の利用者による、間の13版が非表示) | |||
| 10行: | 10行: | ||
三角関数を習っている方ならおなじみとは思いますが、三角関数には角度の加法定理という有名な公式があります。 | 三角関数を習っている方ならおなじみとは思いますが、三角関数には角度の加法定理という有名な公式があります。 | ||
| − | + | この式は複素数の乗算と除算にきわめて関係が深いので、まず最初にこれを紹介しておきます。 | |
| 47行: | 47行: | ||
結局、複素数の積が何を表しているかというと | 結局、複素数の積が何を表しているかというと | ||
| − | # | + | #複素数の積の絶対値は、被乗数と乗数のそれぞれの絶対値の積である。 |
| − | # | + | #複素数の積の実軸からの角度は、被乗数と乗数のそれぞれの実軸からの角度の和になっている。 |
実にシンプルな関係です。では今度は除算に行ってみましょう。 | 実にシンプルな関係です。では今度は除算に行ってみましょう。 | ||
| 56行: | 56行: | ||
{{eqnnn|<math> | {{eqnnn|<math> | ||
\begin{array} {ll} | \begin{array} {ll} | ||
| − | \ | + | \dfrac{c_1}{c_2} &= \dfrac{r_1\cos\theta_1 + ir_1\sin\theta_1}{r_2\cos\theta_2 + ir_2\sin\theta_2} \\[16px] |
| − | &= \ | + | &= \dfrac{(r_1\cos\theta_1 + ir_1\sin\theta_1)(r_2\cos\theta_2 - ir_2\sin\theta_2)}{(r_2\cos\theta_2 + ir_2\sin\theta_2)(r_2\cos\theta_2 - ir_2\sin\theta_2)} \\[16px] |
| − | &= \ | + | &= \dfrac{ r_1r_2(\cos\theta_1\cdot \cos\theta_2 + \sin\theta_1\cdot \sin\theta_2) |
| − | +i\cdot r_1r_2(\sin\theta_1\cdot \cos\theta_2 - \cos\theta_1\cdot \sin\theta_2)}{r_2^2} \\ | + | +i\cdot r_1r_2(\sin\theta_1\cdot \cos\theta_2 - \cos\theta_1\cdot \sin\theta_2)}{r_2^2} \\[16px] |
| − | &= \ | + | &= \dfrac{ r_1r_2(\cos(\theta1-\theta2) + i\sin(\theta1-\theta2))}{r_2^2} \\[16px] |
| − | &= \ | + | &= \dfrac{r_1}{r_2}\angle(\theta1-\theta2) |
\end{array} | \end{array} | ||
</math>}} | </math>}} | ||
| 68行: | 68行: | ||
つまり | つまり | ||
| − | # | + | #複素数の商の絶対値は被除数の絶対値を除数の絶対値で割ったものである。 |
| − | # | + | #複素数の商の実軸からの角度は、被除数の実軸からの角度から除数の実軸からの角度を引いたものになる。 |
| − | + | これは積の反対のことを正確に行っているといえるでしょう。 | |
| + | |||
| + | なぜ、こんな、わけのわからなかったややこしい、複素数の乗算と除算がこんなに単純な美しい式になってしまうのか、 | ||
| + | 実のところ私は理解できておりません。単なる偶然なのか、理論的に導かれる必然なのかはわかりませんが、 | ||
| + | 魔法のように思えてなりません。 | ||
| + | |||
| + | 複素数が角度と回転に深く結びついた数であることは確かです。 | ||
| + | |||
| + | |||
| + | 次は'''「[[複素数のまとめ]]」'''へ | ||
2019年1月12日 (土) 22:18時点における最新版
ここまでの解説でようやく準備が整いましたので、複素数の乗算と除算の話を始めます。
角度の加法定理
実はこの話題は 「回転行列と複素数の積」 でも書いたのですが、あちらに飛んでいただくのもめんどうなので再掲します。
三角関数を習っている方ならおなじみとは思いますが、三角関数には角度の加法定理という有名な公式があります。 この式は複素数の乗算と除算にきわめて関係が深いので、まず最初にこれを紹介しておきます。
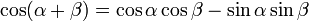
|
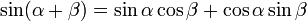
|
簡単ですよね。ここで何となく複素数の乗算に似てるなと思った人もいるかもしれません。ビンゴなのですが、では具体的にどう関係するか見てゆきましょう。
複素数の積と商
二つの複素数、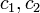 を考えます。それぞれ、絶対値は
を考えます。それぞれ、絶対値は 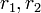 ,
実軸からの角度(方向)は
,
実軸からの角度(方向)は 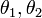 とすると
とすると
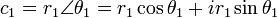
|
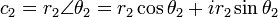
|
この2つの複素数の積をとると
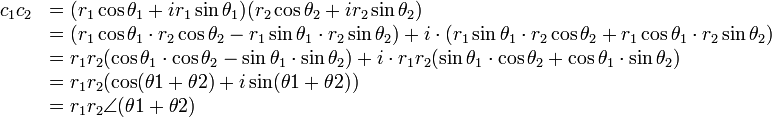
|
3行目で式の中に角度の加法定理の右側が現れたことがお分かりかと思いますが、角度の加法定理を使って式を簡単化すると、 式が驚くほど簡単になってしまいます。
結局、複素数の積が何を表しているかというと
- 複素数の積の絶対値は、被乗数と乗数のそれぞれの絶対値の積である。
- 複素数の積の実軸からの角度は、被乗数と乗数のそれぞれの実軸からの角度の和になっている。
実にシンプルな関係です。では今度は除算に行ってみましょう。
同様に複素数 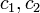 の商を計算すると
の商を計算すると
![\begin{array} {ll}
\dfrac{c_1}{c_2} &= \dfrac{r_1\cos\theta_1 + ir_1\sin\theta_1}{r_2\cos\theta_2 + ir_2\sin\theta_2} \\[16px]
&= \dfrac{(r_1\cos\theta_1 + ir_1\sin\theta_1)(r_2\cos\theta_2 - ir_2\sin\theta_2)}{(r_2\cos\theta_2 + ir_2\sin\theta_2)(r_2\cos\theta_2 - ir_2\sin\theta_2)} \\[16px]
&= \dfrac{ r_1r_2(\cos\theta_1\cdot \cos\theta_2 + \sin\theta_1\cdot \sin\theta_2)
+i\cdot r_1r_2(\sin\theta_1\cdot \cos\theta_2 - \cos\theta_1\cdot \sin\theta_2)}{r_2^2} \\[16px]
&= \dfrac{ r_1r_2(\cos(\theta1-\theta2) + i\sin(\theta1-\theta2))}{r_2^2} \\[16px]
&= \dfrac{r_1}{r_2}\angle(\theta1-\theta2)
\end{array}](/mw/images/math/8/4/e/84e90ffa39122b60b30024e02466a13d.png)
|
つまり
- 複素数の商の絶対値は被除数の絶対値を除数の絶対値で割ったものである。
- 複素数の商の実軸からの角度は、被除数の実軸からの角度から除数の実軸からの角度を引いたものになる。
これは積の反対のことを正確に行っているといえるでしょう。
なぜ、こんな、わけのわからなかったややこしい、複素数の乗算と除算がこんなに単純な美しい式になってしまうのか、 実のところ私は理解できておりません。単なる偶然なのか、理論的に導かれる必然なのかはわかりませんが、 魔法のように思えてなりません。
複素数が角度と回転に深く結びついた数であることは確かです。
次は「複素数のまとめ」へ