「直和」の版間の差分

提供: tknotebook
移動: 案内、 検索
 
6行: 6行:
 
直和の演算が可能なのは、２つのベクトル空間で共通の要素がゼロベクトルのみである場合だけです。この時２つのベクトル空間の和空間を直和といいます。
 
直和の演算が可能なのは、２つのベクトル空間で共通の要素がゼロベクトルのみである場合だけです。この時２つのベクトル空間の和空間を直和といいます。
  
−
和空間とは、ベクトル空間V, W に対して、 ${\bf x} = {\bf v} + {\bf w} ({\bf v} \in V, {\bf w} \in W) $　を満たすすべての要素 からなるベクトル空間です。
+
和空間とは、ベクトル空間V, W に対して、 <math>{\boldsymbol x} = {\boldsymbol v} + {\boldsymbol w} ({\boldsymbol v} \in V, {\boldsymbol w} \in W) </math>　を満たすすべての要素 からなるベクトル空間です。
−
一般に ${\bf x}$に対して${\bf v}$, ${\bf w}$は一意には定まりませんが、和空間が直和の場合、一意に定まります。この時 ${\bf x}$ に対して ${\bf v}$と${\bf w}$を直和分解といいます。
+
一般に <math>{\boldsymbol x}</math>に対して<math>{\boldsymbol v}</math>, <math>{\boldsymbol w}</math>は一意には定まりませんが、和空間が直和の場合、一意に定まります。この時 <math>{\boldsymbol x}</math> に対して <math>{\boldsymbol v}</math>と<math>{\boldsymbol w}</math>を直和分解といいます。

2014年12月29日 (月) 01:54時点における最新版


線形代数の直和(Direct Sum) というのは、２つの部分空間の関係と２つの部分空間から新しい部分空間を作るための演算の両方を表しています。


直和の演算が可能なのは、２つのベクトル空間で共通の要素がゼロベクトルのみである場合だけです。この時２つのベクトル空間の和空間を直和といいます。

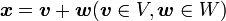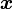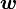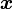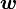和空間とは、ベクトル空間V, W に対して、 {\boldsymbol x} = {\boldsymbol v} + {\boldsymbol w} ({\boldsymbol v} \in V, {\boldsymbol w} \in W) 　を満たすすべての要素 からなるベクトル空間です。 一般に {\boldsymbol x}に対して{\boldsymbol v}, {\boldsymbol w}は一意には定まりませんが、和空間が直和の場合、一意に定まります。この時 {\boldsymbol x} に対して {\boldsymbol v}と{\boldsymbol w}を直和分解といいます。

「http://www.nakamuri.info/mw/index.php?title=直和&oldid=590」から取得