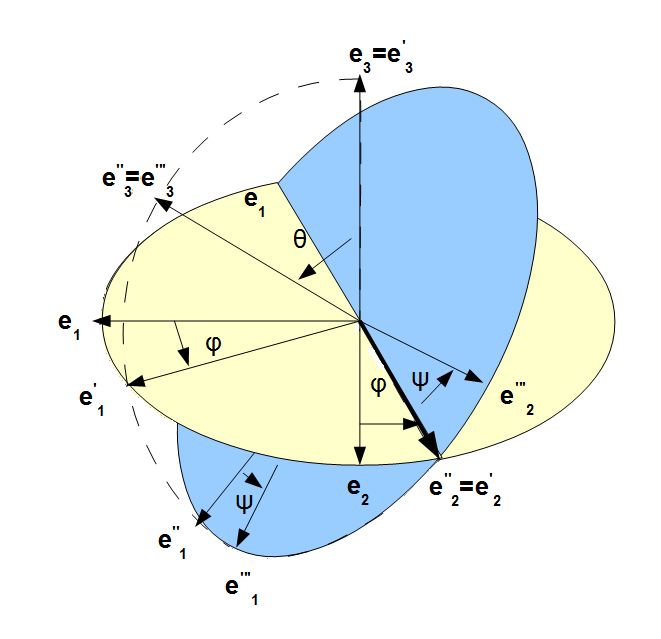
オイラー角
座標の回転を表現する方法には様々な方法がありますが、座標軸を3回回転させるオイラー角が最もポピュラーな方法です。 オイラー角には、回す座標軸の順番によって12種類のバリエーションがあります。飛行機の姿勢を示すのに用いられ、z, y, x軸の順に座標軸を回転させるヨー・ピッチ・ロールは非常に有名ですが(航空業界で用いられているものは、角度の符号が異なります)、ここでは物理で剛体の回転の説明などで使われる Z-Y-Z オイラー角を説明します。
物理や数学で、Z-Y-Z オイラー角が用いられる理由の一つとしてあげられるのは、Z軸の倒し方が、3次元極座標のやり方と一致している点でしょう。
図中の方向ベクトル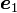 ,
, 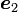 ,
, 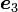 は、座標系の回転を行う前の座標系 xyz座標系の、x, y, z軸の方向ベクトルです。
は、座標系の回転を行う前の座標系 xyz座標系の、x, y, z軸の方向ベクトルです。
Z-Y-Z オイラー角では、まず、z軸(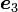 )を軸の正方向に対して右に
)を軸の正方向に対して右に 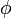 だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが
だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが 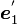 ,
, 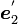 ,
, 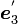 です。
です。
Z-Y-Z オイラー角では、次に、Y'軸(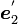 )を軸の正方向に対して右に
)を軸の正方向に対して右に 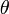 だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが
だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが 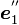 ,
, 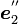 ,
, 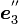 です。
です。
これで、Z''軸(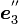 )の向きが定まります。Z''軸の向きは、xyz座標系において、
)の向きが定まります。Z''軸の向きは、xyz座標系において、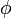 と
と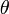 で表される極座標のベクトルの向きと一致しています。
で表される極座標のベクトルの向きと一致しています。
Z-Y-Z オイラー角では、最後に、Z''軸(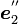 )を軸の正方向に対して右に
)を軸の正方向に対して右に 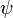 だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが
だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが 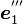 ,
, 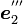 ,
, 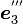 です。
です。
この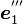 ,
, 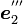 ,
, 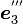 がオイラー角による回転後の座標系の座標軸の方向ベクトルです。
がオイラー角による回転後の座標系の座標軸の方向ベクトルです。
この回転で、元の座標軸の方向ベクトル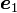 ,
, 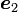 ,
, 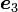 を回転後の座標系の座標軸の方向ベクトル
を回転後の座標系の座標軸の方向ベクトル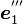 ,
, 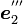 ,
, 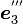 へ移す行列は
へ移す行列は
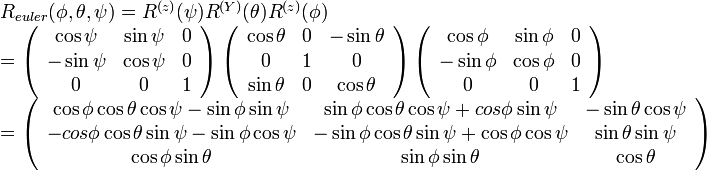
|
( 1 ) |
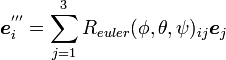
|
( 2 ) |
になります。
座標系 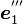 ,
, 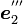 ,
, 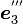 でのベクトル
でのベクトル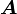 の成分
の成分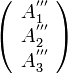 を
座標系
を
座標系 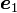 ,
, 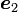 ,
, 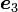 の成分
の成分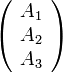 へ変換する式は、
へ変換する式は、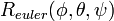 の逆行列(=転置)を使って
の逆行列(=転置)を使って
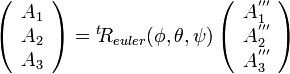
|
( 3 ) |
となります。