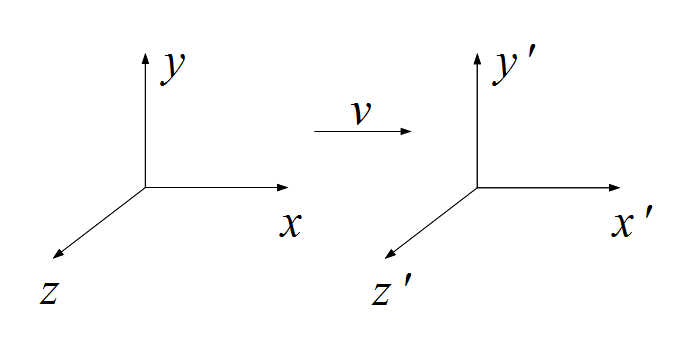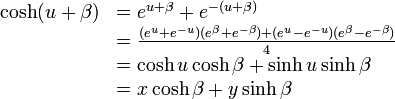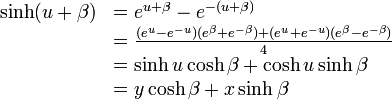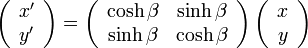「美しいローレンツ変換」の版間の差分
(→双曲線回転) |
(→双曲線回転) |
||
| 142行: | 142行: | ||
[[ファイル:双曲線回転.png]] | [[ファイル:双曲線回転.png]] | ||
| − | 点A の座標は <math>A=(x, y)=(\cosh u, \sinh u)</math> | + | 点A の座標は <math>A=(x, y)=(\cosh u, \sinh u)</math> で、点B は <math>B=(x', y')=(\cosh (u+\beta), \sinh (u+\beta))</math> ですが |
| 150行: | 150行: | ||
\cosh(u+\beta)&=e^{u+\beta} + e^{-(u+\beta)} \\ | \cosh(u+\beta)&=e^{u+\beta} + e^{-(u+\beta)} \\ | ||
&=\frac{(e^{u}+e^{-u})(e^{\beta}+e^{-\beta}) + (e^{u}-e^{-u})(e^{\beta}-e^{-\beta})}{4}\\ | &=\frac{(e^{u}+e^{-u})(e^{\beta}+e^{-\beta}) + (e^{u}-e^{-u})(e^{\beta}-e^{-\beta})}{4}\\ | ||
| − | &=\cosh u \cosh\beta + \sinh u \sinh\beta | + | &=\cosh u \cosh\beta + \sinh u \sinh\beta \\ |
&=x \cosh\beta + y \sinh\beta | &=x \cosh\beta + y \sinh\beta | ||
\end{array} | \end{array} | ||
| 160行: | 160行: | ||
\sinh(u+\beta)&=e^{u+\beta} - e^{-(u+\beta)} \\ | \sinh(u+\beta)&=e^{u+\beta} - e^{-(u+\beta)} \\ | ||
&=\frac{(e^{u}-e^{-u})(e^{\beta}+e^{-\beta}) + (e^{u}+e^{-u})(e^{\beta}-e^{-\beta})}{4}\\ | &=\frac{(e^{u}-e^{-u})(e^{\beta}+e^{-\beta}) + (e^{u}+e^{-u})(e^{\beta}-e^{-\beta})}{4}\\ | ||
| − | &=\sinh u \cosh\beta + \cosh u \sinh\beta | + | &=\sinh u \cosh\beta + \cosh u \sinh\beta \\ |
&=y \cosh\beta + x \sinh\beta | &=y \cosh\beta + x \sinh\beta | ||
\end{array} | \end{array} | ||
| 166行: | 166行: | ||
| + | 以上を整理し、点A(<math>A=(x, y)</math> ) を 点B(<math>A=(x', y')</math> ) に変換する形にまとめると | ||
| + | |||
| + | {{eqn| | ||
| + | <math> | ||
| + | |||
| + | \left( \begin{array} {c} x' \\ y'\end{array}\right) = | ||
| + | \left( \begin{array} {c c} \cosh\beta & \sinh\beta \\ \sinh\beta & \cosh\beta \end{array}\right) | ||
| + | \left( \begin{array} {c} x \\ y\end{array}\right) | ||
| + | |||
| + | </math>|14}} | ||
| + | |||
| + | 式の中央にある行列が、既にローレンツ変換にも出てきた双曲回転の回転行列です。 | ||
| + | |||
| + | この行列は、双曲線 <math>x^2 - y^2 = 1</math> 上の点だけではなく、任意の双曲線 <math>x^2 - y^2 = a^2</math> 形式の双曲線上での双曲回転にも使えます。図は、双曲線 <math>x^2 - y^2 = 1.5^2</math> 上の点C が同じ回転行列で 点D に移動することを示しています。 | ||
'''以下鋭意作成中。''' | '''以下鋭意作成中。''' | ||
2016年3月6日 (日) 08:12時点における版
相対性理論のローレンツ変換は、なんかゴチャゴチャしていてめんどくさそうと感じておられる方も多いと思います。
この点に関して、実はキャンベルの「時空の幾何学」という相対性理論の解説書の中で、その美しさが詳細に述べられていたのですが、
残念ながら邦訳は何故か絶版になってしまいました。
そこで、この記事では、このローレンツ変換の秘められた美しさについて説明します。
ローレンツ変換
下図は、特殊相対性理論を説明するための図です。この図には 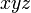 と
と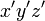 の二つの座標系が示されています。
の二つの座標系が示されています。
相対性理論ではおなじみの座標系の設定ですが、
両座標系とも慣性系で、それぞれの座標系の時刻 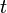 と
と 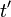 が
が 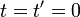 の時、2つの座標系の原点が
一致(重なる)ものとします。
の時、2つの座標系の原点が
一致(重なる)ものとします。
また、座標軸 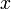 と座標軸
と座標軸 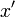 、座標軸
、座標軸 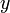 と座標軸
と座標軸 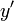 、座標軸
、座標軸 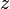 と座標軸
と座標軸 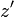 はそれぞれ同じ向きとし、
はそれぞれ同じ向きとし、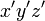 座標系は
座標系は 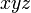 座標系の対し、
座標系の対し、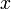 軸方向に速度
軸方向に速度 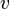 で運動しているものとします。
で運動しているものとします。
この二つの座標系では、相対性理論でおなじみのローレンツ変換の関係が成り立ちます。  は光速とすると
は光速とすると
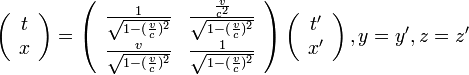
|
( 1 ) |
確かになんかごちゃごちゃしています。真ん中へんにある行列は対称行列でもないし、回転行列のような単純な美しさもありません。 いったいどこが美しいのでしょうか?
ではこれから、ローレンツ変換行列の中に隠された美しさを見てゆきましょう。
座標をちょっといじってみる
ここで、時刻を表すのに、単位が秒の 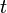 や
や 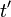 の代わりに、これらに光速をかけた、つまり単位をメートルにした値を時刻に採用します。つまり、時刻の単位を秒ではなく、メートルに変換するのです。
の代わりに、これらに光速をかけた、つまり単位をメートルにした値を時刻に採用します。つまり、時刻の単位を秒ではなく、メートルに変換するのです。
すると、ローレンツ変換は
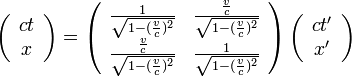
|
( 2 ) |
となります。なんと変換行列が対称行列になってしまいました。最初に比べて美しさが少し増しています。 このことは、時刻が本質的にメートルで表されるべきことを暗示していますが、先に進みましょう。
双曲線関数を使ってみる
式がより簡単になるように、速度 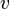 と光速
と光速  の比を
の比を 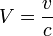 と表すことにすると、
と表すことにすると、
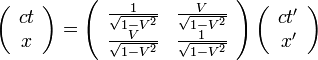
|
( 3 ) |
ここで、 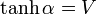 とすると、
とすると、
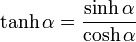
|
( 4 ) |

|
( 5 ) |
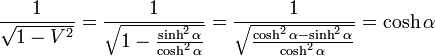
|
( 6 ) |
ですから
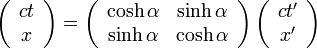
|
( 7 ) |
なんと、まるで回転行列のようなとても単純で覚えやすくて美しい行列になってしまいました。
実はこの行列は双曲線回転の回転行列で、つまりローレンツ変換というのは時空座標の双曲線回転なのです。
以下に双曲線回転の回転行列がどのようなものかを説明します。
そもそも双曲線関数とは
そもそも双曲線関数とは何なのでしょうか?
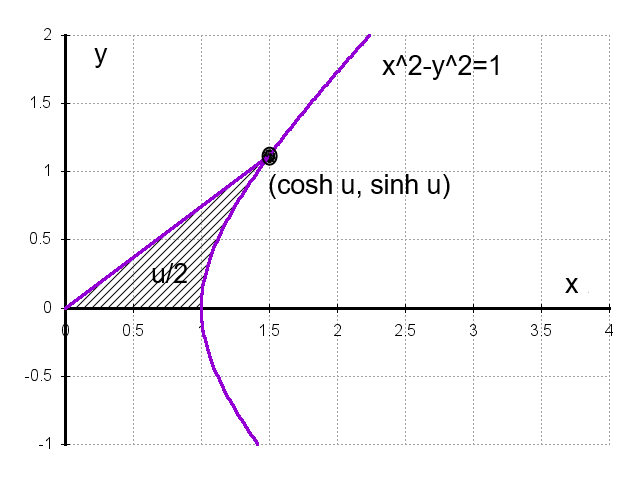
双曲線関数で表すことのできる座標値、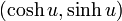 とは双曲線
とは双曲線
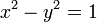
|
( 8 ) |
上の点です。これは公式(5)からも明らかでしょう。それでは 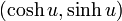 の中の
の中の 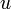 とは何なのでしょうか?
とは何なのでしょうか?
下の図を見てください。
図の斜線の部分は双曲線と、原点と双曲線上の点 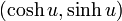 を結んだ線分と、x軸 で囲まれた領域ですが、実はこの領域の面積の2倍が u なのです。証明してみましょう。
を結んだ線分と、x軸 で囲まれた領域ですが、実はこの領域の面積の2倍が u なのです。証明してみましょう。
この領域の面積は 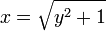 を
を 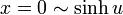 の範囲で積分して、上の三角形部分の面積を引けばよいので
の範囲で積分して、上の三角形部分の面積を引けばよいので
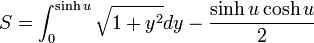
|
( 9 ) |
積分は 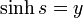 という変数変換を行うと
という変数変換を行うと
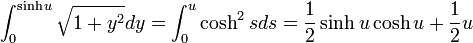
|
( 10 ) |
なので、結局
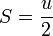
|
( 11 ) |
となります。この面積の2倍( 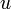 )のことを「双曲角」といいます。
)のことを「双曲角」といいます。
この双曲角と双曲線関数の関係は、半径1の扇形の中心角(扇形の面積の2倍)と三角関数の関係にそっくりです。
そういう意味で、三角関数と双曲線関数はよく似ています。
双曲線回転
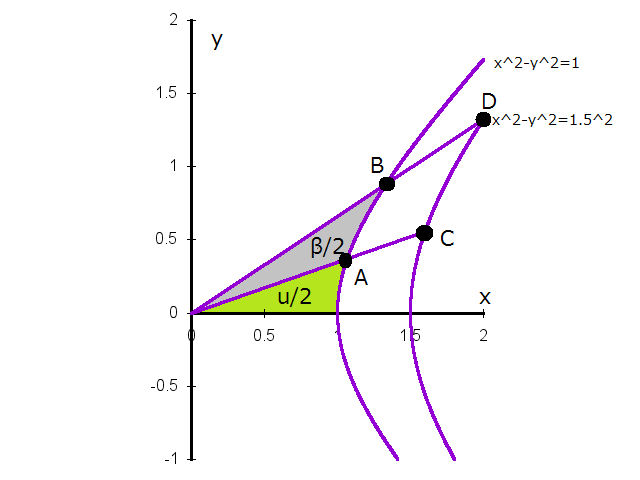
普通の回転が円に沿って座標上の点をを動かすように、双曲線回転は双曲線に沿って座標上の点を動かします。
下の図を見て下さい。図には双曲線 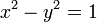 が描いて有り、
その上に双曲角
が描いて有り、
その上に双曲角 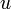 と 構文解析に失敗 (字句解析エラー): u + β
の点 A, B が描いてあります。
任意の双曲線上の点 A を双曲角 βだけ双曲線上を動かす変換を双曲回転といいます。
どのような変換になるか見てみましょう。
と 構文解析に失敗 (字句解析エラー): u + β
の点 A, B が描いてあります。
任意の双曲線上の点 A を双曲角 βだけ双曲線上を動かす変換を双曲回転といいます。
どのような変換になるか見てみましょう。
点A の座標は 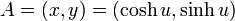 で、点B は
で、点B は 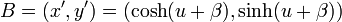 ですが
ですが
|
|
( 12 ) |
|
|
( 13 ) |
以上を整理し、点A(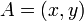 ) を 点B(
) を 点B(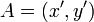 ) に変換する形にまとめると
) に変換する形にまとめると
|
|
( 14 ) |
式の中央にある行列が、既にローレンツ変換にも出てきた双曲回転の回転行列です。
この行列は、双曲線 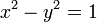 上の点だけではなく、任意の双曲線
上の点だけではなく、任意の双曲線 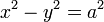 形式の双曲線上での双曲回転にも使えます。図は、双曲線
形式の双曲線上での双曲回転にも使えます。図は、双曲線 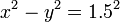 上の点C が同じ回転行列で 点D に移動することを示しています。
上の点C が同じ回転行列で 点D に移動することを示しています。
以下鋭意作成中。