「ラグランジュの運動方程式の導出」の版間の差分
提供: tknotebook
(→一般化座標) |
(→束縛力) |
||
| 26行: | 26行: | ||
と表せます。この独立変数 <math>q_1, q_2, \cdots, q_n</math>を一般化座標といいます。 | と表せます。この独立変数 <math>q_1, q_2, \cdots, q_n</math>を一般化座標といいます。 | ||
| − | == | + | ==束縛条件と束縛力== |
==2つの公式の証明== | ==2つの公式の証明== | ||
==ニュートンの運動方程式からラグランジュの運動方程式へ== | ==ニュートンの運動方程式からラグランジュの運動方程式へ== | ||
2015年6月20日 (土) 08:57時点における版
はじめに
この記事では、ラグランジュの運動方程式を導出の仕方を解説します。
ラグランジュの運動方程式は、系の運動エネルギーと系に加わる力から、系の運動を導き出す運動方程式です。 系の挙動が運動エネルギーと力に集約して描けるのが特徴で、力とたった一つのスカラー関数で系の運動のすべてを記述する美しい方程式です。 系の状態からエネルギーを算出する式が得られれば、機械的に、かつ座標系に依存せず、系の微分方程式を組み立てることができる優れものの手法です。
この記事では、系を互いに影響しあう質点の集合体と捉え、より一般的な一般座標を使い、ニュートンの運動方程式を、座標系に依存しない形のラグランジュの運動方程式に 変換し、ラグランジュの運動方程式が、ニュートン力学と同等であることを示します。
一般化座標
系には N個の質点からできているとします。
各質点のデカルト座標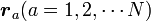は 
、質量は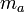 
としましょう。
すると、1個のデカルト座標は3個の座標値を持つので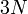 
個の座標値があるわけです。これを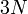個の自由度を持つといいます。
現実の系では、例えば、2個の質点はロープで繋がっていて距離は一定になっちるとか、ある質点は特定の溝に沿って運動しなければ ならないとか、様々な条件の中で動きます。これを束縛条件といいます。
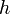個の束縛条件が存在すると、自由度は 
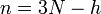個に減少します。これは全ての質点の座標を 
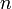個の独立変数で表せることを意味します。つまり、束縛の時間的な変動も考慮すると、質点の座標は
|
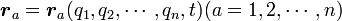
( 1 ) |
と表せます。この独立変数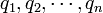 
を一般化座標といいます。
