「ラグランジュの運動方程式の導出」の版間の差分
(→ニュートンの運動方程式からラグランジュの運動方程式へ) |
(→ラグランジュの運動方程式からオイラーラグランジュの運動方程式へ) |
||
| (1人の利用者による、間の80版が非表示) | |||
| 1行: | 1行: | ||
| − | [[メインページ]] > [[物理の部屋]] | + | [[メインページ]] > [[物理の部屋#解析力学]] |
| − | [[category:解析力学]] | + | [[Category:物理]][[category:解析力学]] |
| + | |||
==はじめに== | ==はじめに== | ||
| − | + | この記事では、ラグランジュの運動方程式を導出の仕方を解説します。一般的な説明の仕方ですが、それなりに教科書には書いてないことを加えたつもりなので、多少はお役に立てるかもしれません。 | |
| + | |||
ラグランジュの運動方程式は、系の運動エネルギーと系に加わる力から、系の運動を導き出す運動方程式です。 | ラグランジュの運動方程式は、系の運動エネルギーと系に加わる力から、系の運動を導き出す運動方程式です。 | ||
| − | + | 力とたった一つのスカラー関数で系の運動のすべてを記述する美しい方程式です。 | |
| − | + | 系の状態からエネルギーを算出する式が得られれば、機械的に、かつ座標系に依存せず、系の運動方程式を組み立てることができる優れものの手法です。 | |
| − | + | この記事では、系を互いに影響しあう質点の集合体と捉え、より一般的な一般化座標を使い、ニュートンの運動方程式を、座標系に依存しない形のラグランジュの運動方程式に | |
変換し、ラグランジュの運動方程式が、ニュートン力学と同等であることを示します。 | 変換し、ラグランジュの運動方程式が、ニュートン力学と同等であることを示します。 | ||
| 16行: | 18行: | ||
系はN個の質点からできているとします。 | 系はN個の質点からできているとします。 | ||
| − | 各質点のデカルト座標は <math>{\boldsymbol r_a} \ (a = 1, 2, \cdots N)</math>、質量は <math>m_a \ (a = 1, 2, \cdots N)</math>としましょう。 | + | 各質点のデカルト座標は <math>{\boldsymbol r_a} \ (a = 1, 2, \cdots N)</math>、質量は <math>m_a \ (a = 1, 2, \cdots N)</math>としましょう。<math>a</math>は質点を識別する番号です。 |
| − | + | 1個のデカルト座標は3個の座標値を持ちますので、全質点には <math>3N</math> 個の座標値があります。これを<math>3N</math>個の自由度を持つといいます。 | |
現実の系では、例えば、2個の質点はロープで繋がっていて距離は一定になっているとか、ある質点は特定の溝に沿って運動しなければ | 現実の系では、例えば、2個の質点はロープで繋がっていて距離は一定になっているとか、ある質点は特定の溝に沿って運動しなければ | ||
ならないとか、様々な条件の中で動きます。これを束縛条件といいます。 | ならないとか、様々な条件の中で動きます。これを束縛条件といいます。 | ||
| − | <math>h</math> | + | <math>h</math>個のホロノーム型(後述)束縛条件が存在すると、自由度は <math>n=3N -h</math>個に減少します。これは全ての質点の座標を <math>n</math>個の独立変数で表せることを意味します。つまり、束縛の時間的な変動も考慮すると、質点の座標は |
{{eqn|<math>{\boldsymbol r_a} = {\boldsymbol r_a}(q_1, q_2, \cdots, q_n, t) \ (a=1, 2, \cdots , N)</math>| 1}} | {{eqn|<math>{\boldsymbol r_a} = {\boldsymbol r_a}(q_1, q_2, \cdots, q_n, t) \ (a=1, 2, \cdots , N)</math>| 1}} | ||
| − | と表せます。この独立変数 <math>q_1, q_2, \cdots, q_n</math> | + | と表せます。この独立変数 <math>q_1, q_2, \cdots, q_n</math>を一般化座標と呼びます。 |
==ダランベールの原理と仮想仕事の原理== | ==ダランベールの原理と仮想仕事の原理== | ||
| 37行: | 39行: | ||
となります。 | となります。 | ||
| − | ここで、仮想変位なるものを使います。仮想変位とはもともと静力学の概念で、'''時間の経過を伴わない、質点の実際の運動とは関係のない任意の変位''' | + | ここで、仮想変位なるものを使います。仮想変位とはもともと静力学の概念で、'''時間の経過を伴わない、質点の実際の運動とは関係のない任意の変位'''です。つまり、静力学では、力が釣り合っているかどうかを判断するため、ちょっと仮に動かしてみて、エネルギーが吸収されたり放出されたりしないことを確認します。これを仮想仕事の原理と呼びます。 |
この仮想変位を<math>\delta{\boldsymbol r_a}</math> と表記することにしましょう。 | この仮想変位を<math>\delta{\boldsymbol r_a}</math> と表記することにしましょう。 | ||
| 50行: | 52行: | ||
{{eqn|<math>\sum_a({\boldsymbol F_{m_a}} - m_a\ddot{{\boldsymbol r_a}})\cdot\delta{\boldsymbol r_a} = 0</math>|4}} | {{eqn|<math>\sum_a({\boldsymbol F_{m_a}} - m_a\ddot{{\boldsymbol r_a}})\cdot\delta{\boldsymbol r_a} = 0</math>|4}} | ||
| − | となります。これは元々静力学の原理であった'''仮想仕事の原理'''のダランベールの原理(動力学) | + | となります。これは元々静力学の原理であった'''仮想仕事の原理'''のダランベールの原理(動力学)への拡張です。注意して欲しいのは、この式は、'''束縛条件の範囲内で取りうる任意の'''仮想変位で成り立つということです。 |
| − | '''「仮想変位」''' <math>\delta{\boldsymbol r_a}</math> | + | 解析力学ではこれを一番基本の'''基礎方程式'''とします。 |
| + | |||
| + | '''「仮想変位」''' <math>\delta{\boldsymbol r_a}</math>の3N個の座標値がそれぞれが'''完全に独立'''ならば式(4)は式(2)と同等ですが、仮想変位<math>\delta{\boldsymbol r_a}</math>が後述する束縛条件に従う場合、式(4)は式(2)より条件が甘くなります。このように条件を甘くしてもちゃんと解けるのは、直感的には、'''束縛条件から逸脱した変位がわずかでもあれば、必要な巨大な束縛力が生じ、式(2)が満足され、束縛条件から逸脱した方向の変位が限りなく0に近く抑えられるからです'''。 | ||
| + | |||
| + | このあたりの数学的な厳密な取り扱いは、残念ながら私の手に余ります。 | ||
==束縛条件と束縛力== | ==束縛条件と束縛力== | ||
| 58行: | 64行: | ||
質点の座標の自由度を下げる働きをする「束縛」をもう少し深堀してみましょう。 | 質点の座標の自由度を下げる働きをする「束縛」をもう少し深堀してみましょう。 | ||
| − | + | 束縛には、ホロノーム型と非ホロノーム型の2種類がありますが、ここではホロノーム型の束縛のみを扱います。物理の多くの問題はこのホロノーム型の束縛で扱うことが出来ます。 | |
ホロノーム型の束縛とは、 | ホロノーム型の束縛とは、 | ||
| 64行: | 70行: | ||
{{eqn|<math>G_l({\boldsymbol r_1}, {\boldsymbol r_2}, \cdots, {\boldsymbol r_N}, t)=0\ (l = 1, 2, \cdots h)</math>|5}} | {{eqn|<math>G_l({\boldsymbol r_1}, {\boldsymbol r_2}, \cdots, {\boldsymbol r_N}, t)=0\ (l = 1, 2, \cdots h)</math>|5}} | ||
| − | + | という形でかける束縛のことです。例えば、球が坂を転がり落ちる場合、球は坂に沿って転がるように束縛されます。 | |
| − | + | もし、物体が電車のように決まった軌道に沿って動くように束縛されることも有ります。 | |
| + | |||
| + | こうした束縛は式(5)の形で表わすことができます。 | ||
| + | |||
| + | この坂やレールに沿って物が動く場合、物は坂やレールから、それに沿って動くように力を受けます。この物を束縛条件に沿って運動させる力を束縛力といいます。 | ||
ベクトルを使って物体を扱うニュートン力学では、この束縛力を見積もるのがなかなか大変で、計算が困難なのですが、解析力学では、束縛力をうまく無視することができます。 | ベクトルを使って物体を扱うニュートン力学では、この束縛力を見積もるのがなかなか大変で、計算が困難なのですが、解析力学では、束縛力をうまく無視することができます。 | ||
| − | 例えば、剛体の運動は、本当は剛体の形を保つための原子/ | + | 例えば、剛体の運動は、本当は剛体の形を保つための原子/分子間に働く無数の束縛力を扱わなければならず、無限に等しい個数の運動方程式を解かなければなりません。しかし、解析力学では、束縛力を直接扱わずに式を立てられるため、運動方程式が非常に単純化されます。 |
| 79行: | 89行: | ||
| − | <math>{\boldsymbol F_a}</math> | + | <math>{\boldsymbol F_a}</math>が束縛力以外の力、<math>{\boldsymbol C_a}</math>が束縛力で系の運動を束縛に合わせる力です。束縛力は必ずしも内カ(質点間の作用反作用)ではなく外カの場合もあります。(例: 振り子を支えるカ) |
| 88行: | 98行: | ||
{{eqn|<math>\sum_am_a\ddot{{\boldsymbol r_a}}\cdot\delta{\boldsymbol r_a} = \sum_a({\boldsymbol F_a} + {\boldsymbol C_a})\cdot\delta{\boldsymbol r_a}</math>|7}} | {{eqn|<math>\sum_am_a\ddot{{\boldsymbol r_a}}\cdot\delta{\boldsymbol r_a} = \sum_a({\boldsymbol F_a} + {\boldsymbol C_a})\cdot\delta{\boldsymbol r_a}</math>|7}} | ||
| − | + | となりますが、教科書によっては慣性力と力の釣り合いを強調して | |
{{eqn|<math>\sum_a({\boldsymbol F_a} + {\boldsymbol C_a} - m_a\ddot{{\boldsymbol r_a}}\cdot)\delta{\boldsymbol r_a}=0</math>|8}} | {{eqn|<math>\sum_a({\boldsymbol F_a} + {\boldsymbol C_a} - m_a\ddot{{\boldsymbol r_a}}\cdot)\delta{\boldsymbol r_a}=0</math>|8}} | ||
| 94行: | 104行: | ||
と書くことが多いです。 | と書くことが多いです。 | ||
| − | + | 束縛力にはおもしろい性質が有ります。それは'''束縛力は仕事をしない'''ということです。この点について少し考えてみましょう。例えば垂直抗力は変位の方向と力が垂直ですし、ロープの張力はロープの両端で張力によるエネルギーの得失が発生して正味0になります。しかしこのことは、より一般的な、式(5)に従うことで発生する一般的な束縛力でも成り立つのでしょうか? そもそも束縛条件から束縛力はどのように決まるのでしょうか? | |
| − | + | 束縛条件式(5)の関数<math>G_l</math>は常にゼロですから、仮想変位に対する変化量も当然ゼロです。<math>\delta r_{a, i}</math>が質点<math>a</math>の仮想変位の各軸(i=1⇒x座標, i=2⇒y座標, i=3⇒z座標) の成分を表すとすると、仮想変位に対する<math>G_l</math>の変化量は以下の式であらわされます。 | |
{{eqn|<math>\sum_{a, i}\frac{\partial G_l}{\partial r_{a, i}}\delta r_{a, i}=0 \ (i=1,2,3 \ \ l=1, \cdots , h)</math>|9}} | {{eqn|<math>\sum_{a, i}\frac{\partial G_l}{\partial r_{a, i}}\delta r_{a, i}=0 \ (i=1,2,3 \ \ l=1, \cdots , h)</math>|9}} | ||
| − | これは、<math>\frac{\partial G_l}{\partial r_{a, i}}</math> | + | これは、<math>\frac{\partial G_l}{\partial r_{a, i}}</math>を要素とする3N次元の多次元ベクトルと、<math>r_{a, i}</math>を要素とする3N次元の多次元ベクトル<math>\delta{\boldsymbol R}</math>の内積と考えることができます。 |
| − | つまり、仮想変位<math>\delta{\boldsymbol R}</math> | + | つまり、仮想変位<math>\delta{\boldsymbol R}</math>は3N次元空間の超曲面<math>G_l=0</math>に垂直な多次元ベクトル成分を含みませんから、質点に加わる力のうち、超曲面<math>G_l=0 \ \ (l=1, \cdots, h)</math>に垂直な方向(広義の法線ベクトル)を基底とする部分空間のベクトル方向の力は仕事をしません。これを束縛力(<math>{\boldsymbol C_a}</math>)と定義してやれば、束縛力は必然的に仕事をしないことになります。つまり'''束縛力とは質点にかかる力のうち、式(5)を満足する全ての超曲面の法線ベクトルの一次結合方向成分ということになります。 |
| − | + | これは広義の垂直抗力と呼んでよいでしょう。 | |
| + | |||
| + | 例えば1個の質点がデカルト座標で経路に制限を受ける場合、束縛 <math>G_l</math> が1個なら、束縛(可能な経路)を表す曲面に垂直な力が束縛力です。 | ||
| + | 束縛 <math>G_l</math> が2個なら、束縛(可能な経路)を表す曲線に対して垂直な力が束縛力です。 | ||
| + | |||
| + | 以上の定義から、束縛力は'''束縛によって動きが制限された仮想変位'''<math>\delta{\boldsymbol r_a}</math>に対して仕事をしませんから | ||
{{eqn|<math>\sum_a {\boldsymbol C_a}\cdot\delta{\boldsymbol r_a} = 0</math>|10}} | {{eqn|<math>\sum_a {\boldsymbol C_a}\cdot\delta{\boldsymbol r_a} = 0</math>|10}} | ||
| 112行: | 127行: | ||
{{eqn|<math>\sum_r \left ( \sum_a {\boldsymbol C_a}\cdot \frac{\partial {\boldsymbol r_a}}{\partial q_r} \right )\delta q_r = 0\ (r=1,2,\cdots, n)</math>|11}} | {{eqn|<math>\sum_r \left ( \sum_a {\boldsymbol C_a}\cdot \frac{\partial {\boldsymbol r_a}}{\partial q_r} \right )\delta q_r = 0\ (r=1,2,\cdots, n)</math>|11}} | ||
| + | |||
| + | 式(11)の添え字の <math>r</math> は一般化座標の番号です。 | ||
| + | 位置ベクトルの <math>{\boldsymbol r_a} </math> や 位置の座標 <math>r_{a,i} </math>とは別物ですのでご注意を | ||
<math>\delta q_r</math>は束縛の影響を受けず、完全に独立ですから、任意の <math>\delta q_r</math>で式(11)が成り立つことを考えると、カッコの内側は 常に 0 になるので | <math>\delta q_r</math>は束縛の影響を受けず、完全に独立ですから、任意の <math>\delta q_r</math>で式(11)が成り立つことを考えると、カッコの内側は 常に 0 になるので | ||
| 132行: | 150行: | ||
{{eqn|<math> | {{eqn|<math> | ||
| − | \frac{\partial {\boldsymbol r_a}}{\partial q_r} = \frac{\partial \dot{{\boldsymbol r_a}}}{\ | + | \frac{\partial {\boldsymbol r_a}}{\partial q_r} = \frac{\partial \dot{{\boldsymbol r_a}}}{\partial {\dot q_r}} |
</math>|14}} | </math>|14}} | ||
| − | + | で、一般座標の変化に対する質点の座標の変化率は、一般座標の変化速度の変化に対する質点の速度の変化率は等しい という直観的にはすぐに正しそうだとわかる公式です。 | |
| − | 証明はとても簡単で、<math>{\boldsymbol r_a}</math> | + | 証明はとても簡単で、<math>{\boldsymbol r_a}</math>を時間で微分すると |
| + | |||
| + | ここで時間で微分するとは <math>{\boldsymbol r_a}</math> が時間のみの関数であるとして微分することです。 | ||
| + | つまり <math>{\boldsymbol r_a}</math> 関数の独立変数が全て時間の関数だとして微分を行うのです。 | ||
| + | これは物理数学の暗黙の了解事項なので、戸惑わないようにしてください。 | ||
{{eqn|<math>\dot{\boldsymbol r_a}=\sum_s\frac{\partial {\boldsymbol r_a}}{\partial q_s}\dot q_s + \frac{\partial {\boldsymbol r_a}}{\partial t}</math>|15}} | {{eqn|<math>\dot{\boldsymbol r_a}=\sum_s\frac{\partial {\boldsymbol r_a}}{\partial q_s}\dot q_s + \frac{\partial {\boldsymbol r_a}}{\partial t}</math>|15}} | ||
| 150行: | 172行: | ||
</math>|16}} | </math>|16}} | ||
| − | これは、<math>r_a</math> に関して一般座標の偏微分と時間微分の順番を入れ替えてもよいということを表していますが、これは式(15) | + | これは、<math>r_a</math> に関して一般座標の偏微分と時間微分の順番を入れ替えてもよいということを表していますが、これは式(15)を<math>q_r</math>で偏微分すると |
{{eqn|<math> | {{eqn|<math> | ||
| 189行: | 211行: | ||
</math>|19}} | </math>|19}} | ||
| − | + | すべての質点の運動エネルギーの合計は <math>\ \ T = \sum_a \frac{m_a}{2}\dot{\boldsymbol r_a}^2</math> なので | |
{{eqn|<math> | {{eqn|<math> | ||
| 197行: | 219行: | ||
式(13)の右辺を | 式(13)の右辺を | ||
| − | {{eqn|<math> \ | + | {{eqn|<math> \sum_a{\boldsymbol F_a}\cdot\frac{\partial {\boldsymbol r_a}}{\partial q_r} = f_r</math>|21}} |
とすると、式(13)は | とすると、式(13)は | ||
| 206行: | 228行: | ||
| − | これが''ラグランジュの運動方程式'' | + | これが'''ラグランジュの運動方程式'''です。ちなみに右辺の <math>f_r</math> は一般化座標の変位と掛け合わせてエネルギーを生み出すものなので'''「一般化力」'''という名が付いています。 |
| + | 覚えておいて下さい。 | ||
| + | |||
| + | ==ラグランジュの運動方程式からオイラーラグランジュの運動方程式へ== | ||
| + | |||
| + | ここまでは、単純に外力をそのまま使ってきましたが、ここで <math> {\boldsymbol F_a}</math> を | ||
| + | 保存力 <math>{\boldsymbol F_{\alpha_a}}</math> と 非保存力 | ||
| + | <math>{\boldsymbol F_{\beta_a}}</math> に分けてみましょう。 | ||
| + | 保存力とは <math>{\mathrm rot} {\boldsymbol F_{\alpha_a}}={\boldsymbol 0}</math> となる力場のことです。 | ||
| + | |||
| + | {{eqn|<math> {\boldsymbol F_a}={\boldsymbol F_{\alpha_a}} + {\boldsymbol F_{\beta_a}} \ (a=1, 2, \cdots , N) </math>|23}} | ||
| + | |||
| + | 保存力は ポテンシャル <math>V</math> を使って、質点 <math>a</math> にかかる保存力 <math>{\boldsymbol F_{\alpha_a}}</math> の各座標方向成分(<math>x, y, z</math>方向の値) <math> F_{\alpha_a, i}</math> を計算すると | ||
| + | |||
| + | {{eqn|<math> F_{\alpha_a, i} = - \frac{\partial}{\partial r_{a, i}}V({\boldsymbol r_1}, {\boldsymbol r_2}, \cdots, {\boldsymbol r_N}, t) \ \ \ (i = 1, 2, 3)</math>|24}} | ||
| + | |||
| + | と書くことができますが | ||
| + | |||
| + | {{eqn|<math> \frac{\partial}{\partial q_r}V({\boldsymbol r_1}, {\boldsymbol r_2}, \cdots, {\boldsymbol r_N}, t) =\sum_{i=1,2,3}\sum^N_{a=1} \frac{\partial V}{\partial r_{a, i}} \frac{r_{a, i}}{q_r} = -\sum^N_{a=1}{\boldsymbol F_{\alpha_a}}\cdot \frac{\partial {\boldsymbol r_a}}{\partial q_r}</math>|25}} | ||
| + | |||
| + | は保存力の一般化力のマイナス1倍であることがわかります。 | ||
| + | |||
| + | 従って、このポテンシャルエネルギーを使って | ||
| + | |||
| + | {{eqn|<math>L=T-V</math>|26}} | ||
| + | |||
| + | という、'''ラグランジュ関数(ラグランジアン)''' なるものを定義すると、ラグランジュの方程式は | ||
| + | |||
| + | {{eqn|<math> | ||
| + | \frac{d}{dt}\frac{\partial L}{\partial \dot{q_r}} - \frac{\partial L}{\partial q_r} = \sum^N_{a=1}{\boldsymbol F_{\beta_a}}\cdot \frac{\partial {\boldsymbol r_a}}{\partial q_r} = f_{\beta_r} | ||
| + | </math>|27}} | ||
| + | |||
| + | と変形できます。<math>f_{\beta_r}</math>は外力のうち、非保存力の部分の一般化力です。 | ||
| + | 保存力は ラグランジアン <math>L</math>に吸収されてしまいました。 | ||
| + | |||
| + | 特に外力に非保存力がない場合は、つまり、外力がポテンシャルエネルギーのみで表すことができる場合は | ||
| + | |||
| + | {{eqn|<math> | ||
| + | \frac{d}{dt}\frac{\partial L}{\partial \dot{q_r}} - \frac{\partial L}{\partial q_r} = 0 | ||
| + | </math>|28}} | ||
| + | |||
| + | となります。この形の運動方程式を、'''オイラーラグランジュの運動方程式'''と言います。 | ||
2017年1月22日 (日) 08:14時点における最新版
目次
はじめに
この記事では、ラグランジュの運動方程式を導出の仕方を解説します。一般的な説明の仕方ですが、それなりに教科書には書いてないことを加えたつもりなので、多少はお役に立てるかもしれません。
ラグランジュの運動方程式は、系の運動エネルギーと系に加わる力から、系の運動を導き出す運動方程式です。
力とたった一つのスカラー関数で系の運動のすべてを記述する美しい方程式です。
系の状態からエネルギーを算出する式が得られれば、機械的に、かつ座標系に依存せず、系の運動方程式を組み立てることができる優れものの手法です。
この記事では、系を互いに影響しあう質点の集合体と捉え、より一般的な一般化座標を使い、ニュートンの運動方程式を、座標系に依存しない形のラグランジュの運動方程式に 変換し、ラグランジュの運動方程式が、ニュートン力学と同等であることを示します。
一般化座標
系はN個の質点からできているとします。
各質点のデカルト座標は 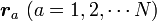 、質量は
、質量は 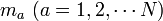 としましょう。
としましょう。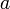 は質点を識別する番号です。
は質点を識別する番号です。
1個のデカルト座標は3個の座標値を持ちますので、全質点には 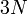 個の座標値があります。これを
個の座標値があります。これを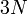 個の自由度を持つといいます。
個の自由度を持つといいます。
現実の系では、例えば、2個の質点はロープで繋がっていて距離は一定になっているとか、ある質点は特定の溝に沿って運動しなければ ならないとか、様々な条件の中で動きます。これを束縛条件といいます。
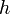 個のホロノーム型(後述)束縛条件が存在すると、自由度は
個のホロノーム型(後述)束縛条件が存在すると、自由度は 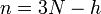 個に減少します。これは全ての質点の座標を
個に減少します。これは全ての質点の座標を 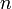 個の独立変数で表せることを意味します。つまり、束縛の時間的な変動も考慮すると、質点の座標は
個の独立変数で表せることを意味します。つまり、束縛の時間的な変動も考慮すると、質点の座標は
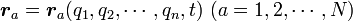
|
( 1 ) |
と表せます。この独立変数 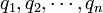 を一般化座標と呼びます。
を一般化座標と呼びます。
ダランベールの原理と仮想仕事の原理
系の各質点にかかる力を 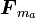 とすると、ニュートンの運動方程式は
とすると、ニュートンの運動方程式は
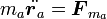
|
( 2 ) |
となります。
ここで、仮想変位なるものを使います。仮想変位とはもともと静力学の概念で、時間の経過を伴わない、質点の実際の運動とは関係のない任意の変位です。つまり、静力学では、力が釣り合っているかどうかを判断するため、ちょっと仮に動かしてみて、エネルギーが吸収されたり放出されたりしないことを確認します。これを仮想仕事の原理と呼びます。
この仮想変位を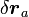 と表記することにしましょう。
と表記することにしましょう。
ニュートンの運動方程式を力と「慣性力」の釣り合いと考え
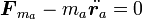
|
( 3 ) |
とします。これがダランベールの原理ですが、式(3)と「仮想変位」 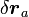 との内積を取り、全質点の総和を取ると、
つまり、力と慣性力が仮想変位に対して行う仕事の総和を計算すると
との内積を取り、全質点の総和を取ると、
つまり、力と慣性力が仮想変位に対して行う仕事の総和を計算すると
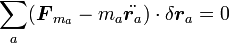
|
( 4 ) |
となります。これは元々静力学の原理であった仮想仕事の原理のダランベールの原理(動力学)への拡張です。注意して欲しいのは、この式は、束縛条件の範囲内で取りうる任意の仮想変位で成り立つということです。
解析力学ではこれを一番基本の基礎方程式とします。
「仮想変位」 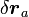 の3N個の座標値がそれぞれが完全に独立ならば式(4)は式(2)と同等ですが、仮想変位
の3N個の座標値がそれぞれが完全に独立ならば式(4)は式(2)と同等ですが、仮想変位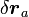 が後述する束縛条件に従う場合、式(4)は式(2)より条件が甘くなります。このように条件を甘くしてもちゃんと解けるのは、直感的には、束縛条件から逸脱した変位がわずかでもあれば、必要な巨大な束縛力が生じ、式(2)が満足され、束縛条件から逸脱した方向の変位が限りなく0に近く抑えられるからです。
が後述する束縛条件に従う場合、式(4)は式(2)より条件が甘くなります。このように条件を甘くしてもちゃんと解けるのは、直感的には、束縛条件から逸脱した変位がわずかでもあれば、必要な巨大な束縛力が生じ、式(2)が満足され、束縛条件から逸脱した方向の変位が限りなく0に近く抑えられるからです。
このあたりの数学的な厳密な取り扱いは、残念ながら私の手に余ります。
束縛条件と束縛力
質点の座標の自由度を下げる働きをする「束縛」をもう少し深堀してみましょう。
束縛には、ホロノーム型と非ホロノーム型の2種類がありますが、ここではホロノーム型の束縛のみを扱います。物理の多くの問題はこのホロノーム型の束縛で扱うことが出来ます。
ホロノーム型の束縛とは、
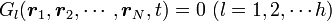
|
( 5 ) |
という形でかける束縛のことです。例えば、球が坂を転がり落ちる場合、球は坂に沿って転がるように束縛されます。
もし、物体が電車のように決まった軌道に沿って動くように束縛されることも有ります。
こうした束縛は式(5)の形で表わすことができます。
この坂やレールに沿って物が動く場合、物は坂やレールから、それに沿って動くように力を受けます。この物を束縛条件に沿って運動させる力を束縛力といいます。
ベクトルを使って物体を扱うニュートン力学では、この束縛力を見積もるのがなかなか大変で、計算が困難なのですが、解析力学では、束縛力をうまく無視することができます。
例えば、剛体の運動は、本当は剛体の形を保つための原子/分子間に働く無数の束縛力を扱わなければならず、無限に等しい個数の運動方程式を解かなければなりません。しかし、解析力学では、束縛力を直接扱わずに式を立てられるため、運動方程式が非常に単純化されます。
ニュートンの運動方程式を、束縛力も含めて考えてみましょう。質点にかかる力 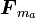 を2つの力
を2つの力 に分けて式(6)のように書き直します。
に分けて式(6)のように書き直します。
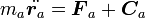
|
( 6 ) |
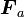 が束縛力以外の力、
が束縛力以外の力、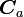 が束縛力で系の運動を束縛に合わせる力です。束縛力は必ずしも内カ(質点間の作用反作用)ではなく外カの場合もあります。(例: 振り子を支えるカ)
が束縛力で系の運動を束縛に合わせる力です。束縛力は必ずしも内カ(質点間の作用反作用)ではなく外カの場合もあります。(例: 振り子を支えるカ)
ここで、束縛力とは何なのか、そもそもどのように定義できるのかを考えてみましょう。
式を仮想仕事の原理の形に書き換えると
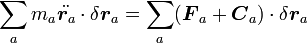
|
( 7 ) |
となりますが、教科書によっては慣性力と力の釣り合いを強調して
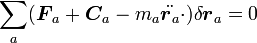
|
( 8 ) |
と書くことが多いです。
束縛力にはおもしろい性質が有ります。それは束縛力は仕事をしないということです。この点について少し考えてみましょう。例えば垂直抗力は変位の方向と力が垂直ですし、ロープの張力はロープの両端で張力によるエネルギーの得失が発生して正味0になります。しかしこのことは、より一般的な、式(5)に従うことで発生する一般的な束縛力でも成り立つのでしょうか? そもそも束縛条件から束縛力はどのように決まるのでしょうか?
束縛条件式(5)の関数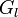 は常にゼロですから、仮想変位に対する変化量も当然ゼロです。
は常にゼロですから、仮想変位に対する変化量も当然ゼロです。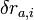 が質点
が質点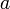 の仮想変位の各軸(i=1⇒x座標, i=2⇒y座標, i=3⇒z座標) の成分を表すとすると、仮想変位に対する
の仮想変位の各軸(i=1⇒x座標, i=2⇒y座標, i=3⇒z座標) の成分を表すとすると、仮想変位に対する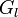 の変化量は以下の式であらわされます。
の変化量は以下の式であらわされます。
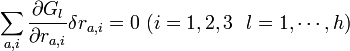
|
( 9 ) |
これは、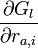 を要素とする3N次元の多次元ベクトルと、
を要素とする3N次元の多次元ベクトルと、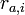 を要素とする3N次元の多次元ベクトル
を要素とする3N次元の多次元ベクトル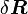 の内積と考えることができます。
の内積と考えることができます。
つまり、仮想変位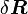 は3N次元空間の超曲面
は3N次元空間の超曲面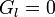 に垂直な多次元ベクトル成分を含みませんから、質点に加わる力のうち、超曲面
に垂直な多次元ベクトル成分を含みませんから、質点に加わる力のうち、超曲面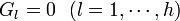 に垂直な方向(広義の法線ベクトル)を基底とする部分空間のベクトル方向の力は仕事をしません。これを束縛力(
に垂直な方向(広義の法線ベクトル)を基底とする部分空間のベクトル方向の力は仕事をしません。これを束縛力(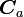 )と定義してやれば、束縛力は必然的に仕事をしないことになります。つまり束縛力とは質点にかかる力のうち、式(5)を満足する全ての超曲面の法線ベクトルの一次結合方向成分ということになります。
)と定義してやれば、束縛力は必然的に仕事をしないことになります。つまり束縛力とは質点にかかる力のうち、式(5)を満足する全ての超曲面の法線ベクトルの一次結合方向成分ということになります。
これは広義の垂直抗力と呼んでよいでしょう。
例えば1個の質点がデカルト座標で経路に制限を受ける場合、束縛 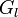 が1個なら、束縛(可能な経路)を表す曲面に垂直な力が束縛力です。
束縛
が1個なら、束縛(可能な経路)を表す曲面に垂直な力が束縛力です。
束縛 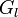 が2個なら、束縛(可能な経路)を表す曲線に対して垂直な力が束縛力です。
が2個なら、束縛(可能な経路)を表す曲線に対して垂直な力が束縛力です。
以上の定義から、束縛力は束縛によって動きが制限された仮想変位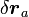 に対して仕事をしませんから
に対して仕事をしませんから
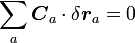
|
( 10 ) |
が成立つはずです。式(1)の関係を使って式(10)を展開すると
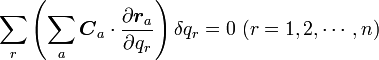
|
( 11 ) |
式(11)の添え字のは一般化座標の番号です。 位置ベクトルの
や 位置の座標
とは別物ですのでご注意を
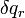 は束縛の影響を受けず、完全に独立ですから、任意の
は束縛の影響を受けず、完全に独立ですから、任意の 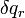 で式(11)が成り立つことを考えると、カッコの内側は 常に 0 になるので
で式(11)が成り立つことを考えると、カッコの内側は 常に 0 になるので
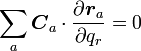
|
( 12 ) |
ということになります。従って、ニュートンの運動方程式は、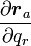 を掛けて全質点の総和を取ると
を掛けて全質点の総和を取ると
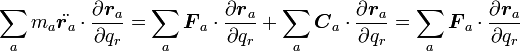
|
( 13 ) |
となり、式の中から束縛力が消えてしまうことが分かります。
2つの公式の証明
ここで、後で使う2つの公式を導いておきます。
最初の公式は
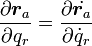
|
( 14 ) |
で、一般座標の変化に対する質点の座標の変化率は、一般座標の変化速度の変化に対する質点の速度の変化率は等しい という直観的にはすぐに正しそうだとわかる公式です。
証明はとても簡単で、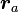 を時間で微分すると
を時間で微分すると
ここで時間で微分するとはが時間のみの関数であるとして微分することです。 つまり
関数の独立変数が全て時間の関数だとして微分を行うのです。 これは物理数学の暗黙の了解事項なので、戸惑わないようにしてください。
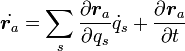
|
( 15 ) |
両辺を 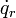 で偏微分すると (14)が得られます。
で偏微分すると (14)が得られます。
次の公式は
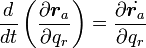
|
( 16 ) |
これは、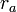 に関して一般座標の偏微分と時間微分の順番を入れ替えてもよいということを表していますが、これは式(15)を
に関して一般座標の偏微分と時間微分の順番を入れ替えてもよいということを表していますが、これは式(15)を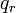 で偏微分すると
で偏微分すると
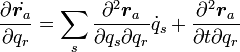
|
( 17 ) |
式(17)の右辺が 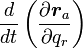 なのは明らかなので、式(16)は証明されました。
なのは明らかなので、式(16)は証明されました。
ニュートンの運動方程式からラグランジュの運動方程式へ
さて必要な公式が整ったところで、ニュートンの運動方程式をラグランジュの運動方程式に一気に持ってゆきましょう。
仮想仕事の式(13)の左辺は
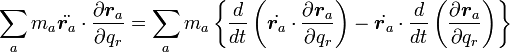
|
( 18 ) |
公式(14)(16)を利用すると
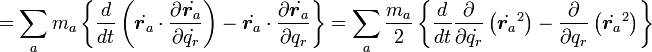
|
( 19 ) |
すべての質点の運動エネルギーの合計は 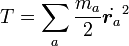 なので
なので
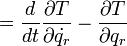
|
( 20 ) |
式(13)の右辺を
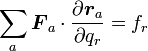
|
( 21 ) |
とすると、式(13)は
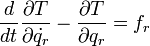
|
( 22 ) |
これがラグランジュの運動方程式です。ちなみに右辺の 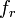 は一般化座標の変位と掛け合わせてエネルギーを生み出すものなので「一般化力」という名が付いています。
覚えておいて下さい。
は一般化座標の変位と掛け合わせてエネルギーを生み出すものなので「一般化力」という名が付いています。
覚えておいて下さい。
ラグランジュの運動方程式からオイラーラグランジュの運動方程式へ
ここまでは、単純に外力をそのまま使ってきましたが、ここで 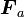 を
保存力
を
保存力 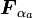 と 非保存力
と 非保存力
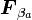 に分けてみましょう。
保存力とは
に分けてみましょう。
保存力とは 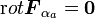 となる力場のことです。
となる力場のことです。
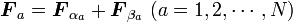
|
( 23 ) |
保存力は ポテンシャル 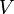 を使って、質点
を使って、質点 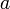 にかかる保存力
にかかる保存力 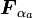 の各座標方向成分(
の各座標方向成分(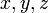 方向の値)
方向の値) 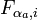 を計算すると
を計算すると
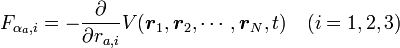
|
( 24 ) |
と書くことができますが
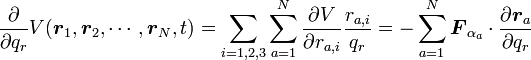
|
( 25 ) |
は保存力の一般化力のマイナス1倍であることがわかります。
従って、このポテンシャルエネルギーを使って
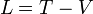
|
( 26 ) |
という、ラグランジュ関数(ラグランジアン) なるものを定義すると、ラグランジュの方程式は
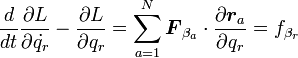
|
( 27 ) |
と変形できます。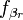 は外力のうち、非保存力の部分の一般化力です。
保存力は ラグランジアン
は外力のうち、非保存力の部分の一般化力です。
保存力は ラグランジアン 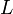 に吸収されてしまいました。
に吸収されてしまいました。
特に外力に非保存力がない場合は、つまり、外力がポテンシャルエネルギーのみで表すことができる場合は
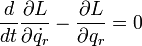
|
( 28 ) |
となります。この形の運動方程式を、オイラーラグランジュの運動方程式と言います。