「幾何学単位系」の版間の差分

提供: tknotebook
移動: 案内、 検索
(→‎幾何学単位系の詳細)
 
(1人の利用者による、間の12版が非表示)
1行: 1行:
 
[[メインページ]] > [[物理の部屋#相対性理論]]
 
[[メインページ]] > [[物理の部屋#相対性理論]]
−
[[category:相対性理論]]
+
[[Category:物理]][[category:相対性理論]]
  
  
16行: 16行:
 
==幾何学単位系の詳細==
 
==幾何学単位系の詳細==
  
−
幾何学単位系は 重力定数、光速、クーロンの法則の係数 <math>\frac{1}{4\pi\varepsilon_0}</math>が 無次元の 1 になるように工夫された単位系です。
+
幾何学単位系は 重力定数、光速、クーロンの法則の係数 <math>\frac{1}{4\pi\varepsilon_0}</math>が 無次元の 1 に( <math> \varepsilon_0=\frac{1}{4\pi} </math> に)なるように工夫された単位系です。
 +
 
 +
<math>\varepsilon_0=1</math> とする流儀もありますが、それは随時補足します。
  
 
幾何学単位系では単位の中に 基本単位として距離の単位である m(メートル) しか出てきません。
 
幾何学単位系では単位の中に 基本単位として距離の単位である m(メートル) しか出てきません。
22行: 24行:
 
ここでは、単位の次元を表す際、習慣に従って距離の単位 m は L と表記することとします。
 
ここでは、単位の次元を表す際、習慣に従って距離の単位 m は L と表記することとします。
  
−
記号 <math>c</math> はSI単位で表した光速を表し <math>299,792,458 m/s</math>
+
記号 <math>c</math> はSI単位で表した光速 <math>299,792,458 m/s</math>
 +
 
 
記号 <math>G</math> はSI単位で表した重力定数 <math>6.673 \times 10^{-11} m^3 kg^{-1} s^{-2}  </math>
 
記号 <math>G</math> はSI単位で表した重力定数 <math>6.673 \times 10^{-11} m^3 kg^{-1} s^{-2}  </math>
 +
 
記号 <math>\varepsilon_0</math>はSI単位で表した真空の誘電率<math>8.85418782\times10^{-12}m^{-3}kg^{-1}s^4A^2</math>
 
記号 <math>\varepsilon_0</math>はSI単位で表した真空の誘電率<math>8.85418782\times10^{-12}m^{-3}kg^{-1}s^4A^2</math>
  
63行: 67行:
  
 
従って、質量はシュバルツシルト半径の半分になります。
 
従って、質量はシュバルツシルト半径の半分になります。
 +
シュバルツシルト半径ではなく、その半分と定義していることに注意!
  
 
{| class="wikitable"
 
{| class="wikitable"
114行: 119行:
 
SI単位系でのクーロンの法則は<math>F=\frac{1}{4\pi\varepsilon}\frac{q_1q_2}{r^2}</math> は幾何学単位系では <math>\frac{1}{4\pi\varepsilon_0}=1</math> なので <math>F=\frac{1}{\varepsilon_r}\frac{q_1q_2}{r^2}</math> になりますが、力が無次元量なので電荷の単位は m になります。
 
SI単位系でのクーロンの法則は<math>F=\frac{1}{4\pi\varepsilon}\frac{q_1q_2}{r^2}</math> は幾何学単位系では <math>\frac{1}{4\pi\varepsilon_0}=1</math> なので <math>F=\frac{1}{\varepsilon_r}\frac{q_1q_2}{r^2}</math> になりますが、力が無次元量なので電荷の単位は m になります。
  
−
力が <math>\frac{G}{c^4}</math> 倍になり、<math>\frac{1}{4\pi\varepsilon_0}=1</math>　になることを考慮すると、電荷は <math>\frac{\sqrt{G}} {c^2  \sqrt{4\pi\varepsilon_0}}</math> 倍 になります。 幾何学単位系では真空の誘電率 <math>\varepsilon_0</math> は <math>\frac{1}{4\pi}</math>になります。
+
力が <math>\frac{G}{c^4}</math> 倍になり、<math>\frac{1}{4\pi\varepsilon_0}=1</math>　になることを考慮すると、電荷は <math>\frac{\sqrt{G}} {c^2  \sqrt{4\pi\varepsilon_0}}</math> 倍 になります。  
−
 
+
 
{| class="wikitable"
 
{| class="wikitable"
 
!SIからの換算係数!!SIへの換算係数!!次元
 
!SIからの換算係数!!SIへの換算係数!!次元
 
|-
 
|-
 
|style="text-align:center" |<math>\frac{\sqrt{G}} {c^2  \sqrt{4\pi\varepsilon_0}}=8.617\times10^{-18}</math> || style="text-align:center" |<math>\frac{c^2  \sqrt{4\pi\varepsilon_0}} {\sqrt{G}}=1.161\times10^{17}</math> || style="text-align:center" |<math>L</math>
 
|style="text-align:center" |<math>\frac{\sqrt{G}} {c^2  \sqrt{4\pi\varepsilon_0}}=8.617\times10^{-18}</math> || style="text-align:center" |<math>\frac{c^2  \sqrt{4\pi\varepsilon_0}} {\sqrt{G}}=1.161\times10^{17}</math> || style="text-align:center" |<math>L</math>
 +
|-
 +
|}
 +
----
 +
<math>\varepsilon_0=1</math> の流儀では
 +
{| class="wikitable"
 +
!SIからの換算係数!!SIへの換算係数!!次元
 +
|-
 +
|style="text-align:center" |<math>\frac{\sqrt{G}} {c^2  \sqrt{\varepsilon_0}}=3.055\times10^{-17}</math> || style="text-align:center" |<math>\frac{c^2  \sqrt{\varepsilon_0}} {\sqrt{G}}=3.274\times10^{16}</math> || style="text-align:center" |<math>L</math>
 
|-
 
|-
 
|}
 
|}

2016年11月9日 (水) 13:09時点における最新版

メインページ > 物理の部屋#相対性理論


はじめに

物理や我々の生活の中で使われる単位系はSI単位系(MKSA単位系)が普通ですが、SI単位系は人間がその生活の中で決めた単位を含んでおり、 物理学に本来不要な換算係数を持ち込むという欠点があります。

ここで紹介する幾何学単位系は、相対性理論の成果を取り込み、相対性理論の式を非常に単純化する単位系です。

幾何単位系の特徴

幾何学単位系の特徴は、何といっても単位に m(メートル) しか出てこないことです。なんと、時間も質量も運動量もエネルギーも単位は m になり、他の単位も全て m を使って記述されます。

幾何学単位系の詳細

幾何学単位系は 重力定数、光速、クーロンの法則の係数 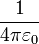\frac{1}{4\pi\varepsilon_0}が 無次元の 1 に( 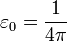\varepsilon_0=\frac{1}{4\pi} に)なるように工夫された単位系です。

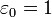\varepsilon_0=1 とする流儀もありますが、それは随時補足します。

幾何学単位系では単位の中に 基本単位として距離の単位である m(メートル) しか出てきません。

ここでは、単位の次元を表す際、習慣に従って距離の単位 m は L と表記することとします。

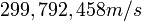
記号 c はSI単位で表した光速 299,792,458 m/s

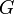記号 G はSI単位で表した重力定数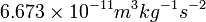 6.673 \times 10^{-11} m^3 kg^{-1} s^{-2}

記号 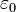\varepsilon_0はSI単位で表した真空の誘電率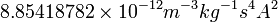8.85418782\times10^{-12}m^{-3}kg^{-1}s^4A^2

を表すこととします。

長さ

SI と同じ m で表されます。何も変わりません。

SIからの換算係数 SIへの換算係数 次元
1 1 L

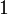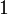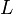
時間

相対性理論の成果を取り入れ、時間と長さは同じ単位になるべきものと考えます。

幾何単位系では 1秒は、その時間での光の飛行距離、つまり 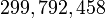299,792,458 m とします。

SIからの換算係数 SIへの換算係数 次元
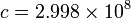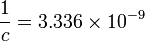c=2.998\times10^8 \frac{1}{c}=3.336\times10^{-9} L

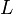
質量

一般相対性理論の成果より、SI単位系での質量とシュバルツシルト半径との関係はSI単位系では

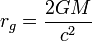
r_g = \frac{2GM}{c^2} 　

この式をそのまま幾何学単位系でも採用し、c=G=1 とすると

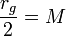
\frac{r_g}{2} = M 　

従って、質量はシュバルツシルト半径の半分になります。 

シュバルツシルト半径ではなく、その半分と定義していることに注意!
SIからの換算係数 SIへの換算係数 次元
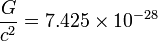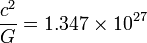\frac{G}{c^2}=7.425\times10^{-28} \frac{c^2}{G}=1.347\times10^{27} L

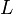
速度

時間の単位が m になったので、時間は c 倍になり、速度は \frac{1}{c}倍になります。

つまり速度は無次元量になり、光速との比になります。


SIからの換算係数 SIへの換算係数 次元
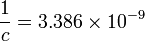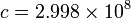\frac{1}{c}=3.386\times10^{-9} c=2.998\times10^8 無

加速度

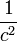時間の単位が m になったので、時間は c 倍になり、加速度は \frac{1}{c^2}倍になります。


SIからの換算係数 SIへの換算係数 次元
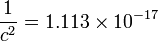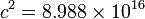\frac{1}{c^2}=1.113\times10^{-17} c^2=8.988\times10^{16} L^{-1}

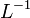
力

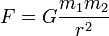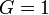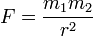F=G\frac{m_1m_2}{r^2} は幾何学単位系では G=1 なので F=\frac{m_1m_2}{r^2} になりますが、質量と長さがともに単位が m になるので力は無次元量になります。

質量は 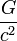\frac{G}{c^2} 倍になることを考慮すると、力は 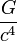\frac{G}{c^4} 倍 になります。

SIからの換算係数 SIへの換算係数 次元
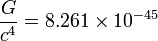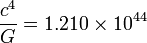\frac{G}{c^4}=8.261\times10^{-45} \frac{c^4}{G}=1.210\times10^{44} 無

電荷

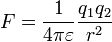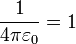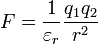SI単位系でのクーロンの法則はF=\frac{1}{4\pi\varepsilon}\frac{q_1q_2}{r^2} は幾何学単位系では \frac{1}{4\pi\varepsilon_0}=1 なので F=\frac{1}{\varepsilon_r}\frac{q_1q_2}{r^2} になりますが、力が無次元量なので電荷の単位は m になります。

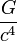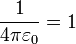力が \frac{G}{c^4} 倍になり、\frac{1}{4\pi\varepsilon_0}=1　になることを考慮すると、電荷は 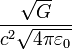\frac{\sqrt{G}} {c^2 \sqrt{4\pi\varepsilon_0}} 倍 になります。

SIからの換算係数 SIへの換算係数 次元
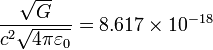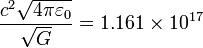\frac{\sqrt{G}} {c^2 \sqrt{4\pi\varepsilon_0}}=8.617\times10^{-18} \frac{c^2 \sqrt{4\pi\varepsilon_0}} {\sqrt{G}}=1.161\times10^{17} L

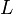
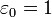\varepsilon_0=1 の流儀では

SIからの換算係数 SIへの換算係数 次元
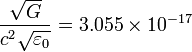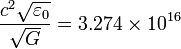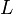
\frac{\sqrt{G}} {c^2 \sqrt{\varepsilon_0}}=3.055\times10^{-17} \frac{c^2 \sqrt{\varepsilon_0}} {\sqrt{G}}=3.274\times10^{16} L
「http://www.nakamuri.info/mw/index.php?title=幾何学単位系&oldid=3405」から取得