「条件付停留値問題」の版間の差分
(→条件付き停留値問題への応用) |
(→条件付き停留値問題への応用) |
||
| (1人の利用者による、間の17版が非表示) | |||
| 1行: | 1行: | ||
[[Category:数学]][[Category:線形代数]][[category:ラグランジュの未定乗数法]] | [[Category:数学]][[Category:線形代数]][[category:ラグランジュの未定乗数法]] | ||
| − | [[メインページ]]>[[数学の部屋 | + | [[メインページ]]>[[数学の部屋#ラグランジュの未定乗数法]] |
==条件付き停留値問題への応用== | ==条件付き停留値問題への応用== | ||
| 7行: | 7行: | ||
これの条件付停留値問題への応用を示しましょう。 | これの条件付停留値問題への応用を示しましょう。 | ||
| − | + | ラグランジュの未定乗数法は、n個のパラメータを持つスカラー関数で説明するのが本来の形ですが、ここではベクトル解析風に説明したいので、以下の説明ではn次元のデカルト座標をベクトルとして入力とするスカラー関数の停留値を考察します。勿論数学的には全く等価です。 | |
| + | ベクトル <math>{\boldsymbol x} = \left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right) </math> の関数 <math>f({\boldsymbol x}) </math> が停留値を持つのは | ||
| + | |||
| + | |||
| + | |||
| + | {{eqn|<math>\mathrm{grad}f({\boldsymbol x}) = 0</math>|1}} | ||
| − | |||
の時ですが、 | の時ですが、 | ||
| − | ベクトル | + | ベクトル <math>{\boldsymbol x} = \left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right) </math> に対し、K個の条件(拘束条件) |
| − | |||
| − | + | {{eqn|<math> G_l({\boldsymbol x}) = 0 (l=1 \sim K)</math>|2}} | |
| − | + | がある場合、関数 <math>f({\boldsymbol x})</math> が停留値を取る条件は変わってきます。これを考えてみましょう。 | |
| − | + | <math>{\boldsymbol x}</math> の微小変化量を <math>\delta{\boldsymbol x}=\left(\begin{array}{c} \delta x_1 \\ \delta x_2 \\ \vdots \\ \delta x_n \end{array}\right)</math> とすると、 | |
| − | \mathrm{grad}G_l({\ | + | |
| − | \frac{\partial G_l({\ | + | |
| − | \frac{\partial G_l({\ | + | {{eqn|<math> |
| + | \mathrm{grad}G_l({\boldsymbol x}) = \left(\begin{array}{c} | ||
| + | \frac{\partial G_l({\boldsymbol x})}{\partial x_1} \\ | ||
| + | \frac{\partial G_l({\boldsymbol x})}{\partial x_2} \\ | ||
\vdots \\ | \vdots \\ | ||
| − | \frac{\partial G_l({\ | + | \frac{\partial G_l({\boldsymbol x})}{\partial x_n} \\ |
\end{array}\right) | \end{array}\right) | ||
| − | + | </math>|3}} | |
| − | + | ||
| − | + | {{eqn|<math>\delta G_l({\boldsymbol x}) = \mathrm{grad}G_l({\boldsymbol x})\cdot\delta{\boldsymbol x} = 0 (l=1\sim K)</math>|4}} | |
| − | |||
| − | + | が成り立つようにしか <math>{\boldsymbol x}</math> は変化できません。 | |
| − | + | 関数 <math>f({\boldsymbol x})</math> が停留値を持つということは、<math>{\boldsymbol x}</math> の微小変化量 <math>\delta{\boldsymbol x}=\left(\begin{array}{c} \delta x_1 \\ \delta x_2 \\ \vdots \\ \delta x_n \end{array}\right)</math> に対し <math>f({\boldsymbol x})</math> が変化しないということなので | |
| − | \mathrm{grad}f({\ | + | |
| − | \frac{\partial f({\ | + | |
| − | \frac{\partial f({\ | + | {{eqn|<math> |
| + | \mathrm{grad}f({\boldsymbol x}) = \left(\begin{array}{c} | ||
| + | \frac{\partial f({\boldsymbol x})}{\partial x_1} \\ | ||
| + | \frac{\partial f({\boldsymbol x})}{\partial x_2} \\ | ||
\vdots \\ | \vdots \\ | ||
| − | \frac{\partial f({\ | + | \frac{\partial f({\boldsymbol x})}{\partial x_n} \\ |
\end{array}\right) | \end{array}\right) | ||
| − | |||
| − | |||
| + | </math>|5}} | ||
| − | |||
| − | + | {{eqn|<math>\delta f({\boldsymbol x}) = \mathrm{grad}f({\boldsymbol x})\cdot\delta{\boldsymbol x} = 0 </math>|6}} | |
| − | |||
| − | |||
| − | とかけます。この式の意味は停留値を取るような | + | [[ラグランジュ未定乗数法の基本部分]] で示しましたように、<math>\mathrm{grad}f({\boldsymbol x})</math> は <math>\delta{\boldsymbol x}</math> が所属する部分空間の直交補空間に属します。従って、適当な係数 <math>\lambda_1, \lambda_2, \cdots , \lambda_K</math>を使って |
| − | + | ||
| + | |||
| + | {{eqn|<math> \mathrm{grad}f({\boldsymbol x}) = -\lambda_1\mathrm{grad}G_1({\boldsymbol x}) - \lambda_2\mathrm{grad}G_2({\boldsymbol x})\cdots -\lambda_K\mathrm{grad}G_K({\boldsymbol x})</math>|7}} | ||
| + | |||
| + | |||
| + | とかけます。この式の意味は停留値を取るような <math>{\boldsymbol x}</math> はこの式を満たすということであり、<math>\mathrm{grad}f({\boldsymbol x})</math> が | ||
| + | <math>-\lambda_1\mathrm{grad}G_1({\boldsymbol x}) - \lambda_2\mathrm{grad}G_2({\boldsymbol x})\cdots -\lambda_K\mathrm{grad}G_K({\boldsymbol x})</math> であらわされる部分空間全体になるわけではありません。 | ||
| + | |||
| + | |||
| + | {{eqn|<math>g({\boldsymbol x}) = f({\boldsymbol x}) + \lambda_1 G_1({\boldsymbol x}) + \lambda_2 G_2({\boldsymbol x})\cdots +\lambda_K G_K({\boldsymbol x})</math>|8}} | ||
| + | |||
| − | |||
とすると、 | とすると、 | ||
| − | + | {{eqn|<math>\mathrm{grad}g({\boldsymbol x}) = 0</math>|9}} | |
| − | つまり | + | つまり '''(2)''' と '''(9)''' が停留値の条件となります。式 '''(2)''' と '''(9)''' は <math>n + K</math> 個の方程式を含みますから、 |
| − | 全ての未知数を求められますので、これで十分です。実際、ラグランジュの未定乗数法というのは 式 | + | 全ての未知数を求められますので、これで十分です。実際、ラグランジュの未定乗数法というのは 式 '''(2)''' と '''(9)''' から停留点を求めるのが普通ですが、ここでもうひとひねりしてみましょう。 |
| − | + | <math>\lambda_1, \lambda_2, \cdots , \lambda_K</math> を関数の独立変数とすれば | |
| − | |||
| − | |||
| − | |||
| − | + | {{eqn|<math>h({\boldsymbol x}, \lambda_1, \lambda_2, \cdots , \lambda_K) = f({\boldsymbol x}) + \lambda_1 G_1({\boldsymbol x}) + \lambda_2 G_2({\boldsymbol x})\cdots +\lambda_K G_K({\boldsymbol x}) | |
| + | </math>|10}} | ||
| − | |||
| − | + | と書けます。<math>\frac{\partial h}{\partial \lambda_i} = G_i = 0</math> は拘束条件そのものなので、<math>\mathrm{grad}</math>を <math>\lambda_1, \lambda_2, \cdots , \lambda_K</math> にまで拡張すれば | |
| + | |||
| + | |||
| + | {{eqn|<math>\mathrm{grad}h({\boldsymbol x}, \lambda_1, \lambda_2, \cdots , \lambda_K) = 0</math>|11}} | ||
| + | |||
| + | |||
| + | が <math>f</math> が停留値を持つ条件です。拘束条件は '''(11)''' に取り込まれてしまった上、式 '''(11)''' は独立変数を <math>\lambda_1, \lambda_2, \cdots , \lambda_K</math> にまで拡大した停留点を求める方程式になっています。 | ||
つまり、ラグランジュの未定乗数法は、束縛条件付き停留値問題を束縛条件なしの停留値問題に巧妙に変換するのです。 | つまり、ラグランジュの未定乗数法は、束縛条件付き停留値問題を束縛条件なしの停留値問題に巧妙に変換するのです。 | ||
| 89行: | 104行: | ||
条件付き停留値問題を、条件なし停留値問題に変換する手順は以下の通りです。 | 条件付き停留値問題を、条件なし停留値問題に変換する手順は以下の通りです。 | ||
| − | 1. 元の関数 | + | 1. 元の関数 <math>f({\boldsymbol x})</math> と束縛条件 <math>G_1({\boldsymbol x})=0, G_2({\boldsymbol x})=0, \cdots, G_K({\boldsymbol x})=0</math> から式 |
| − | + | <math>h({\boldsymbol x}, \lambda_1 ,\lambda_2, \cdots, \lambda_K) = f({\boldsymbol x})+ \lambda_1 G_1({\boldsymbol x}) + \lambda_2 G_2({\boldsymbol x}) + \cdots + \lambda_K G_K({\boldsymbol x}) </math> | |
| + | |||
:を作ります。 | :を作ります。 | ||
| − | |||
| − | + | 2. 以下の式より、停留値での <math>{\boldsymbol x}</math> を求めます。 | |
| + | |||
| + | <math> | ||
\frac{\partial h}{\partial x_1} = 0, \frac{\partial h}{\partial x_2} = 0, \cdots, \frac{\partial h}{\partial x_n}=0, \frac{\partial h}{\partial \lambda_1}=0, | \frac{\partial h}{\partial x_1} = 0, \frac{\partial h}{\partial x_2} = 0, \cdots, \frac{\partial h}{\partial x_n}=0, \frac{\partial h}{\partial \lambda_1}=0, | ||
\frac{\partial h}{\partial \lambda_2}=0, \cdots, \frac{\partial h}{\partial \lambda_K} = 0, | \frac{\partial h}{\partial \lambda_2}=0, \cdots, \frac{\partial h}{\partial \lambda_K} = 0, | ||
| − | + | </math> | |
2020年9月14日 (月) 03:28時点における最新版
条件付き停留値問題への応用
ここまでで、ラグランジュの未定乗数法の根本は直交補空間の直交補空間だと述べてきましたが、 これの条件付停留値問題への応用を示しましょう。
ラグランジュの未定乗数法は、n個のパラメータを持つスカラー関数で説明するのが本来の形ですが、ここではベクトル解析風に説明したいので、以下の説明ではn次元のデカルト座標をベクトルとして入力とするスカラー関数の停留値を考察します。勿論数学的には全く等価です。
ベクトル 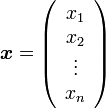 の関数
の関数 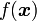 が停留値を持つのは
が停留値を持つのは
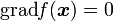
|
( 1 ) |
の時ですが、
ベクトル 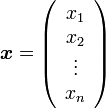 に対し、K個の条件(拘束条件)
に対し、K個の条件(拘束条件)
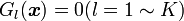
|
( 2 ) |
がある場合、関数 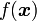 が停留値を取る条件は変わってきます。これを考えてみましょう。
が停留値を取る条件は変わってきます。これを考えてみましょう。
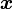 の微小変化量を
の微小変化量を 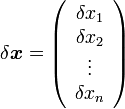 とすると、
とすると、
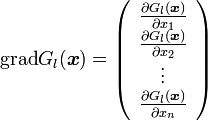
|
( 3 ) |
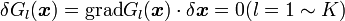
|
( 4 ) |
が成り立つようにしか 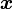 は変化できません。
は変化できません。
関数 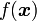 が停留値を持つということは、
が停留値を持つということは、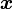 の微小変化量
の微小変化量 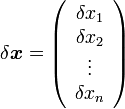 に対し
に対し 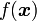 が変化しないということなので
が変化しないということなので
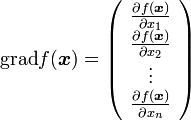
|
( 5 ) |
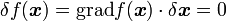
|
( 6 ) |
ラグランジュ未定乗数法の基本部分 で示しましたように、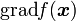 は
は 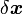 が所属する部分空間の直交補空間に属します。従って、適当な係数
が所属する部分空間の直交補空間に属します。従って、適当な係数 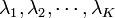 を使って
を使って
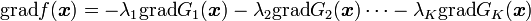
|
( 7 ) |
とかけます。この式の意味は停留値を取るような 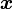 はこの式を満たすということであり、
はこの式を満たすということであり、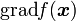 が
が
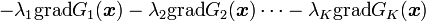 であらわされる部分空間全体になるわけではありません。
であらわされる部分空間全体になるわけではありません。
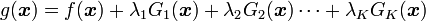
|
( 8 ) |
とすると、
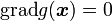
|
( 9 ) |
つまり (2) と (9) が停留値の条件となります。式 (2) と (9) は 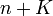 個の方程式を含みますから、
全ての未知数を求められますので、これで十分です。実際、ラグランジュの未定乗数法というのは 式 (2) と (9) から停留点を求めるのが普通ですが、ここでもうひとひねりしてみましょう。
個の方程式を含みますから、
全ての未知数を求められますので、これで十分です。実際、ラグランジュの未定乗数法というのは 式 (2) と (9) から停留点を求めるのが普通ですが、ここでもうひとひねりしてみましょう。
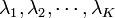 を関数の独立変数とすれば
を関数の独立変数とすれば
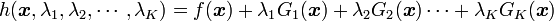
|
( 10 ) |
と書けます。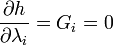 は拘束条件そのものなので、
は拘束条件そのものなので、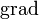 を
を 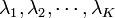 にまで拡張すれば
にまで拡張すれば
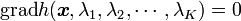
|
( 11 ) |
が 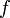 が停留値を持つ条件です。拘束条件は (11) に取り込まれてしまった上、式 (11) は独立変数を
が停留値を持つ条件です。拘束条件は (11) に取り込まれてしまった上、式 (11) は独立変数を 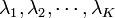 にまで拡大した停留点を求める方程式になっています。
にまで拡大した停留点を求める方程式になっています。
つまり、ラグランジュの未定乗数法は、束縛条件付き停留値問題を束縛条件なしの停留値問題に巧妙に変換するのです。
まとめ
条件付き停留値問題を、条件なし停留値問題に変換する手順は以下の通りです。
1. 元の関数 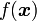 と束縛条件
と束縛条件 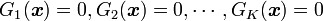 から式
から式
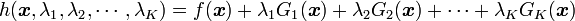
- を作ります。
2. 以下の式より、停留値での 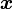 を求めます。
を求めます。