「オイラー角」の版間の差分
| (1人の利用者による、間の21版が非表示) | |||
| 1行: | 1行: | ||
[[Category:数学]][[Category:線形代数]][[category:回転]] | [[Category:数学]][[Category:線形代数]][[category:回転]] | ||
| − | [[メインページ]]>[[数学の部屋 | + | [[メインページ]]>[[数学の部屋#回転]] |
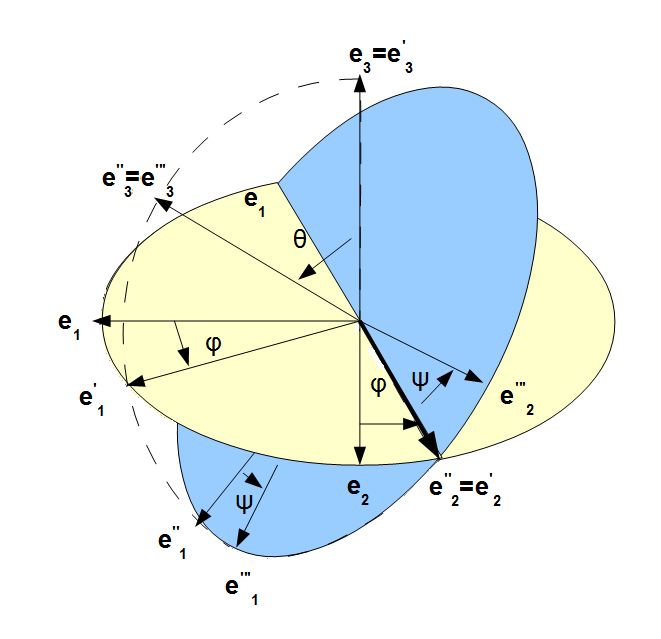
座標の回転を表現する方法には様々な方法がありますが、座標軸を3回回転させるオイラー角が最もポピュラーな方法です。 | 座標の回転を表現する方法には様々な方法がありますが、座標軸を3回回転させるオイラー角が最もポピュラーな方法です。 | ||
| − | オイラー角には、回す座標軸の順番によって12種類のバリエーションがあります。飛行機の姿勢を示すのに用いられ、z, y, | + | オイラー角には、回す座標軸の順番によって12種類のバリエーションがあります。飛行機の姿勢を示すのに用いられ、z, y, x軸の順に座標軸を回転させるヨー・ピッチ・ロールは非常に有名ですが(航空業界で用いられているものは、角度の符号が異なります)、ここでは物理で剛体の回転の説明などで使われる Z-Y-Z オイラー角を説明します。 |
[[ファイル:オイラー角.png]] | [[ファイル:オイラー角.png]] | ||
| 11行: | 11行: | ||
図中の方向ベクトル<math>{\boldsymbol e_1}</math>, <math>{\boldsymbol e_2}</math>, <math>{\boldsymbol e_3}</math>は、座標系の回転を行う前の座標系 xyz座標系の、x, y, z軸の方向ベクトルです。 | 図中の方向ベクトル<math>{\boldsymbol e_1}</math>, <math>{\boldsymbol e_2}</math>, <math>{\boldsymbol e_3}</math>は、座標系の回転を行う前の座標系 xyz座標系の、x, y, z軸の方向ベクトルです。 | ||
| − | |||
| − | Z-Y-Z | + | Z-Y-Z オイラー角では、まず、z軸(<math>{\boldsymbol e_3}</math>)を軸の正方向に対して右に <math>\phi</math>だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが <math>{\boldsymbol e^{'}_1}</math>, <math>{\boldsymbol e^{'}_2}</math>, <math>{\boldsymbol e^{'}_3}</math>です。 |
| − | |||
| − | Z-Y-Z | + | Z-Y-Z オイラー角では、次に、Y'軸(<math>{\boldsymbol e^{'}_2}</math>)を軸の正方向に対して右に <math>\theta</math>だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが <math>{\boldsymbol e^{''}_1}</math>, <math>{\boldsymbol e^{''}_2}</math>, <math>{\boldsymbol e^{''}_3}</math>です。 |
| + | |||
| + | |||
| + | これで、<nowiki>Z''軸</nowiki>(<math>{\boldsymbol e^{''}_3}</math>)の向きが定まります。<nowiki>Z''軸</nowiki>の向きは、xyz座標系において、<math>\phi</math>と<math>\theta</math>で表される極座標のベクトルの向きと一致しています。 | ||
| + | |||
| + | |||
| + | Z-Y-Z オイラー角では、最後に、<nowiki>Z''軸</nowiki>(<math>{\boldsymbol e^{''}_3}</math>)を軸の正方向に対して右に <math>\psi</math>だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが <math>{\boldsymbol e^{'''}_1}</math>, <math>{\boldsymbol e^{'''}_2}</math>, <math>{\boldsymbol e^{'''}_3}</math>です。 | ||
| + | |||
この<math>{\boldsymbol e^{'''}_1}</math>, <math>{\boldsymbol e^{'''}_2}</math>, <math>{\boldsymbol e^{'''}_3}</math>がオイラー角による回転後の座標系の座標軸の方向ベクトルです。 | この<math>{\boldsymbol e^{'''}_1}</math>, <math>{\boldsymbol e^{'''}_2}</math>, <math>{\boldsymbol e^{'''}_3}</math>がオイラー角による回転後の座標系の座標軸の方向ベクトルです。 | ||
| + | |||
この回転で、元の座標軸の方向ベクトル<math>{\boldsymbol e_1}</math>, <math>{\boldsymbol e_2}</math>, <math>{\boldsymbol e_3}</math>を回転後の座標系の座標軸の方向ベクトル<math>{\boldsymbol e^{'''}_1}</math>, <math>{\boldsymbol e^{'''}_2}</math>, <math>{\boldsymbol e^{'''}_3}</math>へ移す行列は | この回転で、元の座標軸の方向ベクトル<math>{\boldsymbol e_1}</math>, <math>{\boldsymbol e_2}</math>, <math>{\boldsymbol e_3}</math>を回転後の座標系の座標軸の方向ベクトル<math>{\boldsymbol e^{'''}_1}</math>, <math>{\boldsymbol e^{'''}_2}</math>, <math>{\boldsymbol e^{'''}_3}</math>へ移す行列は | ||
| + | |||
{{eqn|<math> | {{eqn|<math> | ||
| − | \begin{array}{ | + | \begin{array}{lll} |
R_{euler}(\phi, \theta, \psi) = R^{(z)}(\psi) R^{(Y)}(\theta) R^{(z)}(\phi) \\ | R_{euler}(\phi, \theta, \psi) = R^{(z)}(\psi) R^{(Y)}(\theta) R^{(z)}(\phi) \\ | ||
= | = | ||
| 56行: | 63行: | ||
</math>|1}} | </math>|1}} | ||
| − | + | {{eqn|<math>{\boldsymbol e^{'''}_i}=\sum_{j=1}^3R_{euler}(\phi, \theta, \psi)_{ij}{\boldsymbol e_j}</math>|2}} | |
| + | |||
| + | になります(<math>R_{euler}(\phi, \theta, \psi)_{ij}</math>は<math>R_{euler}(\phi, \theta, \psi)</math>の<math>i</math>行<math>j</math>列の要素)。 | ||
| + | |||
| + | |||
| + | 座標系 <math>{\boldsymbol e^{'''}_1}</math>, <math>{\boldsymbol e^{'''}_2}</math>, <math>{\boldsymbol e^{'''}_3}</math> でのベクトル<math>{\boldsymbol A}</math>の成分<math>\left( \begin{array} {c} A^{'''}_1 \\ A^{'''}_2 \\ A^{'''}_3\end{array}\right)</math>を | ||
| + | 座標系 <math>{\boldsymbol e_1}</math>, <math>{\boldsymbol e_2}</math>, <math>{\boldsymbol e_3}</math>の成分<math>\left( \begin{array} {c} A_1 \\ A_2 \\ A_3\end{array}\right)</math>へ変換する式は、<math>R_{euler}(\phi, \theta, \psi)</math>の逆行列(=転置)を使って | ||
| + | |||
| + | {{eqn|<math> | ||
| + | \left( \begin{array} {c} A_1 \\ A_2 \\ A_3\end{array}\right) = | ||
| + | {}^t\!R_{euler}(\phi, \theta, \psi) | ||
| + | \left( \begin{array} {c} A^{'''}_1 \\ A^{'''}_2 \\ A^{'''}_3\end{array}\right) | ||
| + | </math>|3}} | ||
| + | |||
| + | となります。 | ||
2015年8月5日 (水) 05:25時点における最新版
座標の回転を表現する方法には様々な方法がありますが、座標軸を3回回転させるオイラー角が最もポピュラーな方法です。 オイラー角には、回す座標軸の順番によって12種類のバリエーションがあります。飛行機の姿勢を示すのに用いられ、z, y, x軸の順に座標軸を回転させるヨー・ピッチ・ロールは非常に有名ですが(航空業界で用いられているものは、角度の符号が異なります)、ここでは物理で剛体の回転の説明などで使われる Z-Y-Z オイラー角を説明します。
物理や数学で、Z-Y-Z オイラー角が用いられる理由の一つとしてあげられるのは、Z軸の倒し方が、3次元極座標のやり方と一致している点でしょう。
図中の方向ベクトル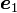 ,
, 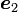 ,
, 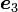 は、座標系の回転を行う前の座標系 xyz座標系の、x, y, z軸の方向ベクトルです。
は、座標系の回転を行う前の座標系 xyz座標系の、x, y, z軸の方向ベクトルです。
Z-Y-Z オイラー角では、まず、z軸(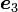 )を軸の正方向に対して右に
)を軸の正方向に対して右に 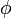 だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが
だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが 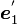 ,
, 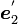 ,
, 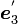 です。
です。
Z-Y-Z オイラー角では、次に、Y'軸(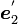 )を軸の正方向に対して右に
)を軸の正方向に対して右に 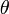 だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが
だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが 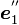 ,
, 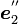 ,
, 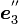 です。
です。
これで、Z''軸(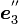 )の向きが定まります。Z''軸の向きは、xyz座標系において、
)の向きが定まります。Z''軸の向きは、xyz座標系において、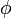 と
と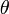 で表される極座標のベクトルの向きと一致しています。
で表される極座標のベクトルの向きと一致しています。
Z-Y-Z オイラー角では、最後に、Z''軸(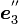 )を軸の正方向に対して右に
)を軸の正方向に対して右に 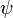 だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが
だけ回します。こうして得られた新しい座標系の座標軸の方向ベクトルが 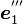 ,
, 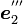 ,
, 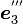 です。
です。
この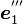 ,
, 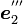 ,
, 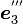 がオイラー角による回転後の座標系の座標軸の方向ベクトルです。
がオイラー角による回転後の座標系の座標軸の方向ベクトルです。
この回転で、元の座標軸の方向ベクトル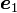 ,
, 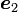 ,
, 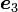 を回転後の座標系の座標軸の方向ベクトル
を回転後の座標系の座標軸の方向ベクトル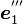 ,
, 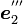 ,
, 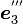 へ移す行列は
へ移す行列は
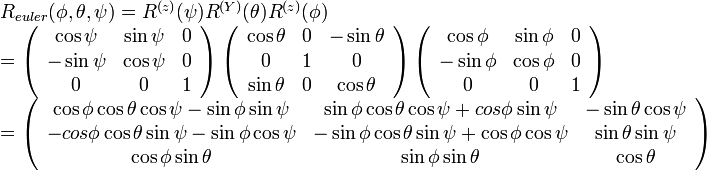
|
( 1 ) |
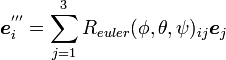
|
( 2 ) |
になります(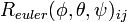 は
は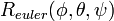 の
の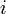 行
行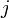 列の要素)。
列の要素)。
座標系 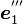 ,
, 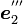 ,
, 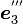 でのベクトル
でのベクトル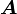 の成分
の成分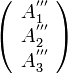 を
座標系
を
座標系 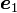 ,
, 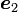 ,
, 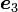 の成分
の成分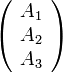 へ変換する式は、
へ変換する式は、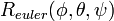 の逆行列(=転置)を使って
の逆行列(=転置)を使って
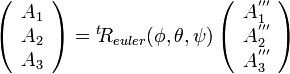
|
( 3 ) |
となります。