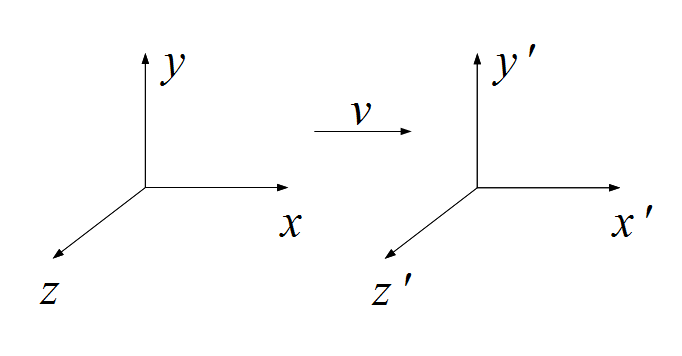「美しいローレンツ変換」の版間の差分
提供: tknotebook
(→ローレンツ変換) |
(→ローレンツ変換) |
||
| 30行: | 30行: | ||
\end{array}\right) | \end{array}\right) | ||
\left( \begin{array} {cc} t'\\ x' \end{array}\right), y=y', z=z'</math>|1}} | \left( \begin{array} {cc} t'\\ x' \end{array}\right), y=y', z=z'</math>|1}} | ||
| + | |||
| + | 確かになんかごちゃごちゃしています。真ん中へんにある行列は対称行列でもないし、回転行列のような単純な美しさもありません。 | ||
| + | いったいどこが美しいのでしょうか? | ||
| + | |||
| + | ではこれから、ローレンツ変換行列の中に隠された美しさを見てゆきましょう。 | ||
| + | |||
| + | ==座標をちょっといじってみる== | ||
2016年3月3日 (木) 13:01時点における版
相対性理論のローレンツ変換は、なんかゴチャゴチャしていてめんどくさそうと感じておられる方も多いと思います。
この点に関して、実はキャンベルの「時空の幾何学」という相対性理論の解説書の中で、その美しさが詳細に述べられていたのですが、
残念ながら邦訳は何故か絶版になってしまいました。
そこで、この記事では、このローレンツ変換の秘められた美しさについて説明します。
ローレンツ変換
下図は、特殊相対性理論を説明するための図です。この図には 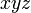 と
と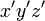 の二つの座標系が示されています。
の二つの座標系が示されています。
相対性理論ではおなじみの座標系の設定ですが、
両座標系とも慣性系で、それぞれの座標系の時刻 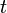 と
と 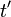 が
が 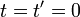 の時、2つの座標系の原点が
一致(重なる)ものとします。
の時、2つの座標系の原点が
一致(重なる)ものとします。
また、座標軸 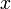 と座標軸
と座標軸 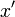 、座標軸
、座標軸 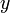 と座標軸
と座標軸 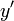 、座標軸
、座標軸 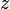 と座標軸
と座標軸 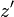 はそれぞれ同じ向きとし、
はそれぞれ同じ向きとし、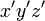 座標系は
座標系は 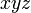 座標系の対し、
座標系の対し、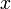 軸方向に速度
軸方向に速度 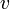 で運動しているものとします。
で運動しているものとします。
この二つの座標系では、相対性理論でおなじみのローレンツ変換の関係が成り立ちます。
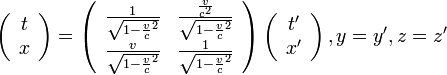
|
( 1 ) |
確かになんかごちゃごちゃしています。真ん中へんにある行列は対称行列でもないし、回転行列のような単純な美しさもありません。 いったいどこが美しいのでしょうか?
ではこれから、ローレンツ変換行列の中に隠された美しさを見てゆきましょう。