「複素数とは?」の版間の差分
提供: tknotebook
(ページの作成:「Category:数学Category:基礎category:複素数 メインページ>数学の部屋#複素数」) |
|||
| 1行: | 1行: | ||
[[Category:数学]][[Category:基礎]][[category:複素数]] | [[Category:数学]][[Category:基礎]][[category:複素数]] | ||
[[メインページ]]>[[数学の部屋#複素数]] | [[メインページ]]>[[数学の部屋#複素数]] | ||
| + | |||
| + | |||
| + | ==おかしな数 複素数 == | ||
| + | |||
| + | 複素数はその最初の紹介のされ方が不気味なせいか、'''まっとうな数に思われていない'''節があります。確かに | ||
| + | |||
| + | {{eqnnn|<math> i \times i = -1 </math>}} | ||
| + | |||
| + | という数 <math>i</math>(虚数) が有るなどといきなり言われても到底納得いかないでしょう。中には | ||
| + | 複素数はまともな数学ではないとはなから受け入れない方もいます。確かに胡散臭いです。でも本当のところ | ||
| + | 複素数は数学のみならず、理学や工学の世界でも幅広く使われている便利な道具であり、よく考えるとそれは | ||
| + | 実数の自然な拡張でもあるのです。 | ||
| + | |||
| + | ==実数と複素数をどう見るべきか?== | ||
| + | |||
| + | 複素数をまっとうな数として受け入れるには少々発想の転換が必要です。 | ||
| + | |||
| + | 簡単に言ってしまえば、数は実は2次元ベクトルであって、実数もその仲間だったとということを受け入れてしまうのです。 | ||
| + | |||
| + | 複素数は簡単に言ってしまえば独特の四則演算規則を備えた2次元ベクトルです。複素数を2次元ベクトル風に <math>(a, b)</math> というように表せば、四則演算規則は | ||
| + | |||
| + | |||
| + | '''1. 加算''' | ||
| + | {{eqnnn|<math>(a, b) + (c, d) = (a+c, b+d) </math>}} | ||
| + | '''2. 減算''' | ||
| + | {{eqnnn|<math>(a, b) - (c, d) = (a-c, b-d) </math>}} | ||
| + | '''3. 掛算''' | ||
| + | {{eqnnn|<math>(a, b) \times (c, d) = (ac-bd, ad+bc) </math>}} | ||
| + | '''3. 割算''' | ||
| + | {{eqnnn|<math>(a, b) \div (c, d) = \left( \frac{ac+bd}{c^2+d^2}, \frac{bc-ad}{c^2+d^2} \right) </math>}} | ||
| + | |||
| + | となります。割り算がやけに複雑ですが、気にしないようにしましょう(^^; | ||
| + | |||
| + | ここで、実数は2次元ベクトルの後ろのほうの数字が 0 の特別な場合、 | ||
| + | つまり <math> (p, 0) = p </math> (<math>p</math>は実数) と定義すると | ||
| + | <math> (p, 0) = p</math> (<math>p</math>は実数) </math>, | ||
| + | <math> (q, 0) = q </math>(<math>q</math>は実数) とすれば、上の計算式から | ||
| + | |||
| + | '''1. 加算''' | ||
| + | {{eqnnn|<math>(p, 0) + (q, 0) = (p+q, 0) = p+q </math>}} | ||
| + | '''2. 減算''' | ||
| + | {{eqnnn|<math>(p, 0) - (q, 0) = (p-q, 0) = p-q</math>}} | ||
| + | '''3. 掛算''' | ||
| + | {{eqnnn|<math>(p, 0) \times (q, 0) = (pq, 0) = pq </math>}} | ||
| + | '''4. 割算''' | ||
| + | {{eqnnn|<math>(p, 0) \div (q, 0) = \left( \frac{pq}{q^2}, \frac{0}{q^2} \right) = \left( \frac{p}{q}, \frac{0}{q^2} \right) = \frac{p}{q} </math>}} | ||
| + | |||
| + | |||
| + | と実数での四則演算は全てそのまま成り立っていますから、複素数演算は、実数の演算を2次元ベクトルに拡張したものであり、 | ||
| + | 複素数は実数を2次元ベクトルの拡張したのもであることが分かります。 | ||
2017年8月7日 (月) 09:35時点における版
おかしな数 複素数
複素数はその最初の紹介のされ方が不気味なせいか、まっとうな数に思われていない節があります。確かに
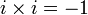
|
という数 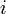 (虚数) が有るなどといきなり言われても到底納得いかないでしょう。中には
複素数はまともな数学ではないとはなから受け入れない方もいます。確かに胡散臭いです。でも本当のところ
複素数は数学のみならず、理学や工学の世界でも幅広く使われている便利な道具であり、よく考えるとそれは
実数の自然な拡張でもあるのです。
(虚数) が有るなどといきなり言われても到底納得いかないでしょう。中には
複素数はまともな数学ではないとはなから受け入れない方もいます。確かに胡散臭いです。でも本当のところ
複素数は数学のみならず、理学や工学の世界でも幅広く使われている便利な道具であり、よく考えるとそれは
実数の自然な拡張でもあるのです。
実数と複素数をどう見るべきか?
複素数をまっとうな数として受け入れるには少々発想の転換が必要です。
簡単に言ってしまえば、数は実は2次元ベクトルであって、実数もその仲間だったとということを受け入れてしまうのです。
複素数は簡単に言ってしまえば独特の四則演算規則を備えた2次元ベクトルです。複素数を2次元ベクトル風に 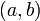 というように表せば、四則演算規則は
というように表せば、四則演算規則は
1. 加算
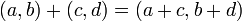
|
2. 減算
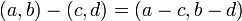
|
3. 掛算
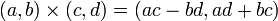
|
3. 割算
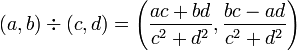
|
となります。割り算がやけに複雑ですが、気にしないようにしましょう(^^;
ここで、実数は2次元ベクトルの後ろのほうの数字が 0 の特別な場合、
つまり 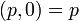 (
(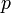 は実数) と定義すると
は実数) と定義すると
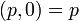 (
(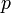 は実数) </math>,
は実数) </math>,
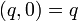 (
(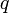 は実数) とすれば、上の計算式から
は実数) とすれば、上の計算式から
1. 加算
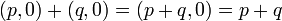
|
2. 減算
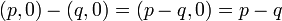
|
3. 掛算
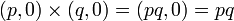
|
4. 割算
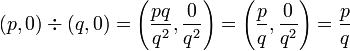
|
と実数での四則演算は全てそのまま成り立っていますから、複素数演算は、実数の演算を2次元ベクトルに拡張したものであり、
複素数は実数を2次元ベクトルの拡張したのもであることが分かります。