「複素数の四則演算の性質」の版間の差分
提供: tknotebook
| 12行: | 12行: | ||
{{eqnnn|<math> (a, b) \times (p, 0) = (pa, pb) </math>}} | {{eqnnn|<math> (a, b) \times (p, 0) = (pa, pb) </math>}} | ||
{{eqnnn|<math> (p, 0) \times (a, b) = (pa, pb) </math>}} | {{eqnnn|<math> (p, 0) \times (a, b) = (pa, pb) </math>}} | ||
| + | |||
| + | 2. 複素数と実数の割り算 | ||
| + | |||
| + | {{eqnnn|<math> (a, b) \div (p, 0) = (\frac{a}{p}, \frac{b}{p}) </math>}} | ||
| + | {{eqnnn|<math> (p, 0) \div (a, b) = \left (\frac{pa}{a^2+b^2}, \frac{-pb}{a^2+b^2} \right) </math>}} | ||
2017年8月7日 (月) 13:14時点における版
ひとつ前の解説「複素数とは?」では、複素数の演算が実数同士の演算を変えないことを示しました。
では複素数と実数ではどのようになるのでしょうか?
加減算は簡単なので、掛け算と除算を示しましょう。
1. 複素数と実数掛け算
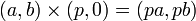
|
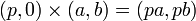
|
2. 複素数と実数の割り算
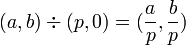
|
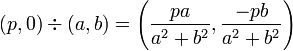
|