「配列の軸」の版間の差分
提供: tknotebook
| 21行: | 21行: | ||
a = np.array( | a = np.array( | ||
| − | + | [ [ [1, 2], [4, 5], [7, 8] ], | |
| − | + | [ [10, 11], [13, 14], [16, 17] ], | |
| − | + | [ [19, 20], [22, 23], [25, 26] ] | |
| − | + | ] | |
) | ) | ||
| − | |||
print(repr(a)) | print(repr(a)) | ||
3次元配列はこんな感じで表示されます。 | 3次元配列はこんな感じで表示されます。 | ||
| − | array([[[ 1, 2 | + | array([[[ 1, 2], |
| − | [ 4, 5 | + | [ 4, 5], |
| − | [ 7, 8 | + | [ 7, 8]], |
| − | [[10, 11 | + | [[10, 11], |
| − | [13, 14 | + | [13, 14], |
| − | [16, 17 | + | [16, 17]], |
| − | [[19, 20 | + | [[19, 20], |
| − | [22, 23 | + | [22, 23], |
| − | [25, 26 | + | [25, 26]]]) |
numpyの ndarray は自身を表示するとき、最も下位の次元の要素を横に並べて表示し、他の次元は縦に並べて表示するので、かなり見にくいです。 | numpyの ndarray は自身を表示するとき、最も下位の次元の要素を横に並べて表示し、他の次元は縦に並べて表示するので、かなり見にくいです。 | ||
| 52行: | 51行: | ||
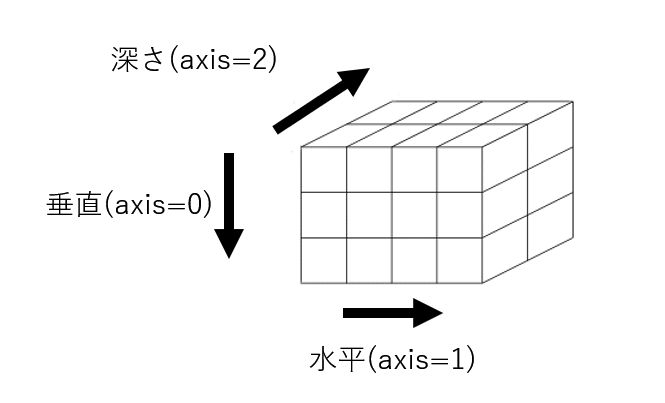
この3次元配列とその配列インデックスの関係を表したものが下図です。 | この3次元配列とその配列インデックスの関係を表したものが下図です。 | ||
| + | |||
| + | [[ファイル:軸.png]] | ||
| + | |||
| + | これは3次元の配列を、小さな立方体を多数集めた直方体で表現したもので、個々の立方体は最下位次元の配列の要素です。 | ||
| + | |||
| + | 垂直とか、水平とか、深さと書いてあるので配列のインデックスのことで、 | ||
| + | |||
| + | 垂直(axis=0) とは3次元配列の最上位の次元のインデックスのこと。 | ||
| + | |||
| + | 水平(axis=1) とは3次元配列の2番目の次元のインデックスのこと。 | ||
| + | |||
| + | 深さ(axis=2) とは3次元配列の3番目(最下位)の次元のインデックスのこと。 | ||
2022年5月4日 (水) 07:37時点における版
メインページ>コンピュータの部屋#Python>Numpy Tips
Numpy を使用していると axis というパラメータによく出くわしますが、
あまりよい解説がなく戸惑う人が多いと思います。
そこで「軸(axis)」を簡単に説明してみようと思います。
多次元配列
用語等を解説したいので、とりあえず3次元配列を中心に話を進めます。
まず、3×3×3(shape = (3, 3, 3)) の配列を作ってみます。
python の REPL にこんなコードを入力すると
import numpy as np
a = np.array(
[ [ [1, 2], [4, 5], [7, 8] ],
[ [10, 11], [13, 14], [16, 17] ],
[ [19, 20], [22, 23], [25, 26] ]
]
)
print(repr(a))
3次元配列はこんな感じで表示されます。
array([[[ 1, 2],
[ 4, 5],
[ 7, 8]],
[[10, 11],
[13, 14],
[16, 17]],
[[19, 20],
[22, 23],
[25, 26]]])
numpyの ndarray は自身を表示するとき、最も下位の次元の要素を横に並べて表示し、他の次元は縦に並べて表示するので、かなり見にくいです。
この配列の第1次元の2つ目、第2次元3つ目、第3次元の1つ目にアクセスするには
a[1][2][0]
と書きますが、numpyの配列は
a[1, 2, 0]
とも書けます。便利ですね。もちろん値は 16 になります。
この3次元配列とその配列インデックスの関係を表したものが下図です。
これは3次元の配列を、小さな立方体を多数集めた直方体で表現したもので、個々の立方体は最下位次元の配列の要素です。
垂直とか、水平とか、深さと書いてあるので配列のインデックスのことで、
垂直(axis=0) とは3次元配列の最上位の次元のインデックスのこと。
水平(axis=1) とは3次元配列の2番目の次元のインデックスのこと。
深さ(axis=2) とは3次元配列の3番目(最下位)の次元のインデックスのこと。