「配列の軸」の版間の差分

2022年5月4日 (水) 09:04時点における版

メインページ>コンピュータの部屋#Python>Numpy Tips

Numpy を使用していると axis というパラメータによく出くわしますが、 あまりよい解説がなく戸惑う人が多いと思います。

そこで「軸(axis)」を簡単に説明してみようと思います。

多次元配列

とりあえず3次元配列を中心に話を進めます。

まず、3×3×2(shape = (3, 3, 2)) の配列を作ってみます。

python の REPL にこんなコードを入力すると

import numpy as np

a = np.array(
   [   [   [1, 2], [3, 4], [5, 6]        ],
       [   [7, 8], [9, 10], [11, 12]     ],
       [   [13, 14], [15, 16], [17, 18]  ],
       [   [19, 20], [21, 22], [23, 24]  ]
   ]
)
print(repr(a)) print(repr(a))

3次元配列はこんな感じで表示されます。

array([[[ 1,  2],
       [ 3,  4],
       [ 5,  6]],

      [[ 7,  8],
       [ 9, 10],
       [11, 12]],

      [[13, 14],
       [15, 16],
       [17, 18]],

      [[19, 20],
       [21, 22],
       [23, 24]]])

numpyの ndarray は自身を表示するとき、最も下位の次元の要素を横に並べて表示し、他の次元は縦に並べて表示するので、かなり見にくいです。

この配列の第1次元の２つ目、第２次元の３つ目、第3次元の1つ目の要素にアクセスするには、各次元の配列インデックスを使って

a[1][2][0]

と書きますが、numpyの配列では

a[1, 2, 0]

とも書けます。便利ですね。もちろん値は 11 になります。

軸

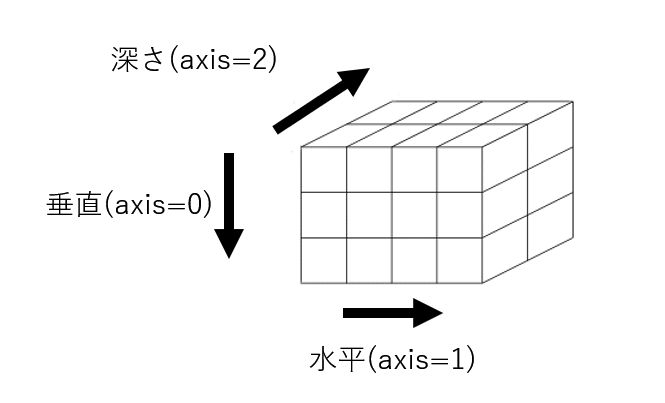
この3次元配列とその配列インデックスの関係を表したものが下図です。

これは3次元の配列を、小さな立方体を多数集めた直方体で表現したもので、個々の立方体は最下位次元の配列の要素です。

垂直とか、水平とか、深さと書いてあるのは配列のインデックスのことで、

axis(軸) とは簡単に言ってしまえば

• 配列のインデクスにつけた番号
• 配列の次元に付けた番号
• インデックスを変化させたときの方向

たいていは関数のパラメータとして、どの次元のインデックスを変化させて処理するかを表していると考えてもよいです。 具体的な意味は、axis をパラメータに取る関数の仕様によりかなり変わってきます。

axis = 0 → 垂直方向のインデックス(vertical) = 1番目(最上位)の次元のインデックス

axis = 1 → 水平方向のインデックス(horizontal) = 2番目の次元のインデックス

axis = 2 → 深さ方向のインデックス(depth) = 3番目(最下位)の次元のインデックス

尚、numpy の解説では 図の深さ方向を axis = 0 と紹介するのが一般的ですが、 軸方向へ配列を連結する np.vstack(axis=0方向), np.hstack(axis=1方向), np.dstack(axis=2方向) 関数の名称を鑑み 奥行方向を axis=2 としました。

これは直方体を見る目の方向の違いであって、どうでもよい話ですが、numpyの関数名称を理解するにはこちらの方が良いです。

4次元以上の配列の軸

4次元以上の配列の立体的な把握は困難なので、 axis(軸)は

1番目の次元のインデックス → axis=0
2番目の次元のインデックス → axis=1
3番目の次元のインデックス → axis=2
4番目の次元のインデックス → axis=3
5番目の次元のインデックス → axis=4

というように覚えておけばよいでしょう。3次元以下の配列でもこれで十分かもしれません。

2次元配列の軸

2次元配列は行列として扱うことが多いですが。その場合 axis(軸) は

axis=0 のインデックス→ 行番号
axis=1 のインデックス→ 列番号

但し軸の表す方向は、行方向, 列方向という意味ではなくて、

axis=0 → 行を横断する方向
axis=1 → 列を横断する方向 = 行方向

なので、混乱しないように。