「ラグランジュ未定乗数法の基本部分」の版間の差分
提供: tknotebook
| 4行: | 4行: | ||
ラグランジュ未定乗数法の基本は意外と簡単なものです。 | ラグランジュ未定乗数法の基本は意外と簡単なものです。 | ||
| − | |||
| − | + | {{eqn|<math>{\boldsymbol a}\cdot{\boldsymbol b}=0</math>|1} | |
| − | + | が任意のベクトル <math>{\boldsymbol b}</math> で成り立つには <math>{\boldsymbol a}= {\boldsymbol 0}</math> であることが必要です。 | |
| − | <math>{\ | + | では、一次独立なベクトル群 <math>{\boldsymbol c_l} (l=1~K)</math> に対し |
| − | + | <math>{\boldsymbol b}\cdot{\boldsymbol c_l}=0 (l=1\sim K) \label{eq3}</math> | |
| − | <math>{\ | + | という制限の中で <math>{\boldsymbol b}</math> が任意であるとき、<math>{\boldsymbol a}</math> はどのような値になり得るかを考えてみましょう。 |
| − | + | ||
| + | <math>{\boldsymbol b}</math> がとり得るベクトルの集合は基底 <math>{\boldsymbol c_l}</math>が張る部分空間の直交補空間であることは定義上明らかです。 | ||
| + | また、<math>{\boldsymbol a}</math> のとり得るベクトルの集合は <math>{\boldsymbol b}</math> のとり得るベクトル集合の直交補空間であることは明らかです。 | ||
| − | |||
| − | <math>{\ | + | つまり、「[[直交補空間]]」の記事で書いたように、<math>{\boldsymbol a}</math>のとり得るベクトル集合は <math>{\boldsymbol c_l}</math> が張る部分空間と同じになるので、 |
| + | |||
| + | <math>{\boldsymbol a}=\lambda_1{\boldsymbol c_1}+\lambda_2{\boldsymbol c_2}+\cdots+\lambda_K{\boldsymbol c_K} \label{eq4}</math> | ||
となるのです。この一次結合の結合係数が実はラグランジュの未定乗数になるのです。 | となるのです。この一次結合の結合係数が実はラグランジュの未定乗数になるのです。 | ||
2014年12月29日 (月) 01:37時点における版
ラグランジュ未定乗数法の基本は意外と簡単なものです。
{{eqn|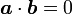 |1}
|1}
が任意のベクトル 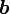 で成り立つには
で成り立つには 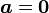 であることが必要です。
であることが必要です。
では、一次独立なベクトル群 構文解析に失敗 (字句解析エラー): {\boldsymbol c_l} (l=1~K)
に対し
構文解析に失敗 (不明な関数「\label」): {\boldsymbol b}\cdot{\boldsymbol c_l}=0 (l=1\sim K) \label{eq3}
という制限の中で 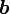 が任意であるとき、
が任意であるとき、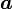 はどのような値になり得るかを考えてみましょう。
はどのような値になり得るかを考えてみましょう。
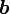 がとり得るベクトルの集合は基底
がとり得るベクトルの集合は基底 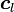 が張る部分空間の直交補空間であることは定義上明らかです。
また、
が張る部分空間の直交補空間であることは定義上明らかです。
また、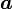 のとり得るベクトルの集合は
のとり得るベクトルの集合は 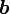 のとり得るベクトル集合の直交補空間であることは明らかです。
のとり得るベクトル集合の直交補空間であることは明らかです。
つまり、「直交補空間」の記事で書いたように、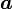 のとり得るベクトル集合は
のとり得るベクトル集合は 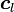 が張る部分空間と同じになるので、
が張る部分空間と同じになるので、
構文解析に失敗 (不明な関数「\label」): {\boldsymbol a}=\lambda_1{\boldsymbol c_1}+\lambda_2{\boldsymbol c_2}+\cdots+\lambda_K{\boldsymbol c_K} \label{eq4}
となるのです。この一次結合の結合係数が実はラグランジュの未定乗数になるのです。
次ページ 条件付停留値問題 へ