「座標変換と回転」の版間の差分
(→座標軸の方向ベクトルの変換) |
(→座標軸の方向ベクトルの変換) |
||
| 56行: | 56行: | ||
{{eqn|<math>A^'_i=\sum_{j=1}^3({\boldsymbol e^'_i}\cdot{\boldsymbol e_j})A_j = \sum_{j=1}^3R_{ij}A_j</math>|9}} | {{eqn|<math>A^'_i=\sum_{j=1}^3({\boldsymbol e^'_i}\cdot{\boldsymbol e_j})A_j = \sum_{j=1}^3R_{ij}A_j</math>|9}} | ||
| − | つまり、'''行列<math>R_{ij}</math>は xyz座標系での座標の'''成分'''をx'y'z'座標系の成分に変換する行列'''でもあります。 | + | これを省略せずにすべて書くと |
| + | |||
| + | {{eqn|<math> | ||
| + | \left( \begin{array} {c} A^'_1 \\ A^'_2 \\ A^'_3\end{array}\right) = | ||
| + | \left( \begin{array} {ccc} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{array}\right) | ||
| + | \left( \begin{array} {c} A_1 \\ A_2 \\ A_3\end{array}\right) | ||
| + | </math>|10}} | ||
| + | |||
| + | つまり、'''行列<math>(R_{ij})</math>は xyz座標系での座標の'''成分'''をx'y'z'座標系の成分に変換する行列'''でもあります。 | ||
2015年6月10日 (水) 17:36時点における版
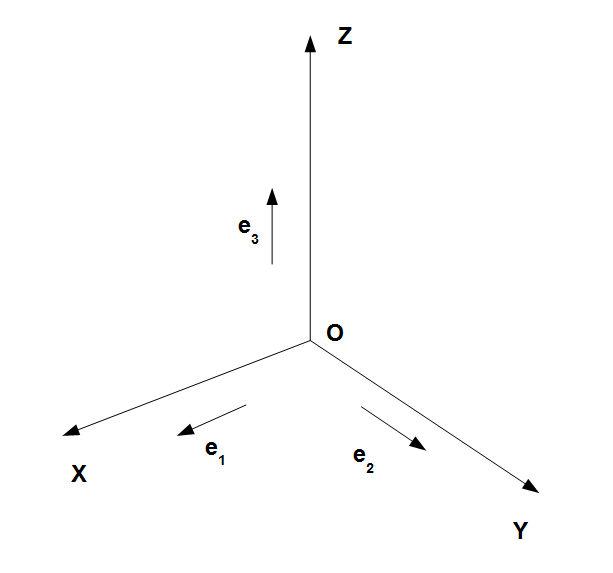
座標系の定義
座標というのは空間上に定められた目盛のというか定規のようなものと考えてよいでしょう。ここではデカルト座標(直交座標)に話を絞ります。
デカルト座標は基準となる原点と、X, Y, Z方向を下の図のように定めるとひとつ定義できます。
図の点Oが座標の原点を表します。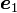 ,
, 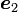 ,
, 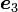 は、x軸, y軸, z軸の方向を表す方向ベクトル(単位ベクトル)で、デカルト座標なので互いに直交しています。
は、x軸, y軸, z軸の方向を表す方向ベクトル(単位ベクトル)で、デカルト座標なので互いに直交しています。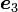 は、
は、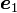 が回転して
が回転して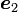 に向くとき、その回転に対して右ネジの方向に定めます。これを「右手系」といいます。
に向くとき、その回転に対して右ネジの方向に定めます。これを「右手系」といいます。
デカルト座標上での点の位置 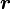 の座標値(成分)は
の座標値(成分)は
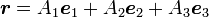
|
( 1 ) |
と定義します。つまり、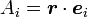 という関係になります。
という関係になります。
え!、点O や、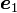 ,
, 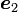 ,
, 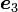 はどういう座標系を使って定義するんだって? それは神様が定義した座標があるとしましょう。だって、座標系の定義に座標系が必要だと、話が永遠に終わらないからです(^^;
はどういう座標系を使って定義するんだって? それは神様が定義した座標があるとしましょう。だって、座標系の定義に座標系が必要だと、話が永遠に終わらないからです(^^;
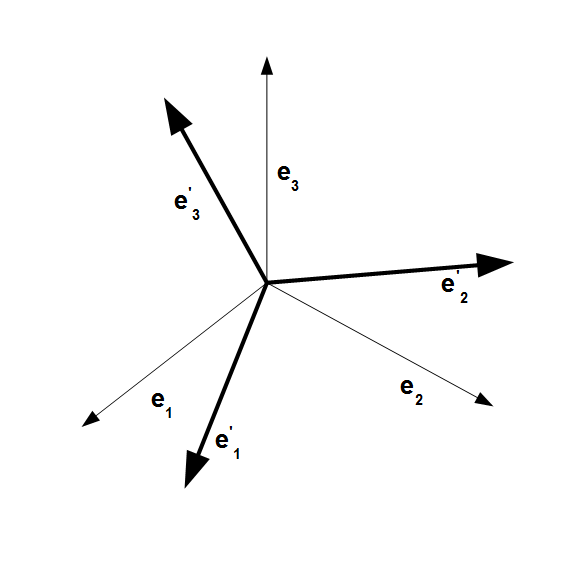
座標軸の方向ベクトルの変換
次に原点が一致する2つの異なるデカルト座標系の座標変換を考えます。
図には xyz座標系と x'y'z' 座標系の2つが示されていますが 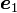 ,
, 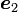 ,
, 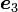 が xyz座標系の座標軸の方向ベクトルを、
が xyz座標系の座標軸の方向ベクトルを、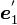 ,
, 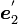 ,
, 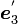 が x'y'z'座標系の座標軸の方向ベクトルを表しています。
が x'y'z'座標系の座標軸の方向ベクトルを表しています。
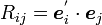
|
( 2 ) |
とし、x'y'z' 座標系の座標軸の方向ベクトル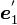 ,
, 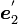 ,
, 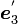 をxyz座標系の成分で表すと、
をxyz座標系の成分で表すと、
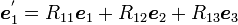
|
( 3 ) |
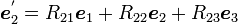
|
( 4 ) |
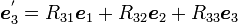
|
( 5 ) |
これは以下のように略記できます。
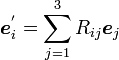
|
( 6 ) |
ここで 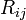 を
を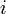 行
行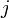 列の要素に持つ行列を
列の要素に持つ行列を 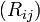 と書くことにしましょう。
と書くことにしましょう。
この 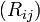 は座標系の座標軸方向ベクトルを別の座標軸方向ベクトルへ移すための行列です。
は座標系の座標軸方向ベクトルを別の座標軸方向ベクトルへ移すための行列です。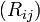 の各行ベクトルは x'y'z座標系の座標軸の方向ベクトルを xyz座標系の成分で表したものですから、各行ベクトルの大きさは1であり、各行ベクトルは互いに直交することは明らかでしょう。また逆変換は
の各行ベクトルは x'y'z座標系の座標軸の方向ベクトルを xyz座標系の成分で表したものですから、各行ベクトルの大きさは1であり、各行ベクトルは互いに直交することは明らかでしょう。また逆変換は  と
と を入れ替えた、つまり転置になることは明らかなので、
を入れ替えた、つまり転置になることは明らかなので、 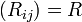 とすると
とすると
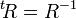
|
( 7 ) |
になります。
ベクトル 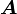 を2つの座標系の成分で表すと
を2つの座標系の成分で表すと
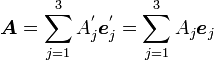
|
( 8 ) |
両辺に 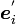 をかけると
をかけると
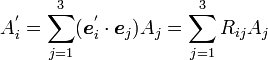
|
( 9 ) |
これを省略せずにすべて書くと
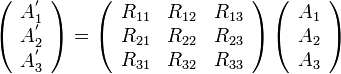
|
( 10 ) |
つまり、行列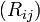 は xyz座標系での座標の成分をx'y'z'座標系の成分に変換する行列でもあります。
は xyz座標系での座標の成分をx'y'z'座標系の成分に変換する行列でもあります。