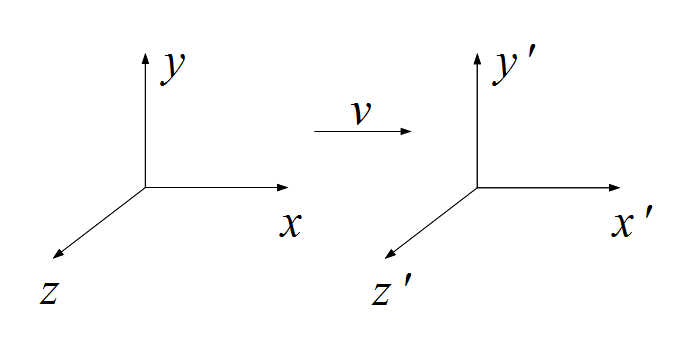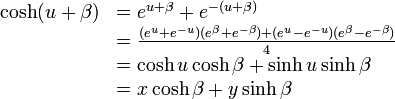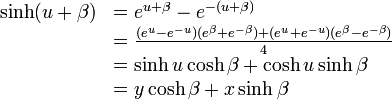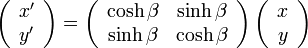「美しいローレンツ変換」の版間の差分
(→目盛りの大きさ) |
(→目盛りの大きさ) |
||
| 309行: | 309行: | ||
OFの <math>tx</math> 座標系での長さは | OFの <math>tx</math> 座標系での長さは | ||
| − | {{eqn|OFの長さ <math>=\sqrt{1+\tanh^2\alpha}=\frac{\cosh | + | {{eqn|OFの長さ <math>=\sqrt{1+\tanh^2\alpha}=\frac{\sqrt{\cosh 2\alpha}}{\cosh\alpha}=\sqrt{1+V^2}</math>|19}} |
従って OF の<math>t'x'</math> 座標系での長さは | 従って OF の<math>t'x'</math> 座標系での長さは | ||
| 320行: | 320行: | ||
このように、系の中で静止している棒がもう一つの系から見ると短く見えるのは、ガレージのパラドックスとして有名ですが、同じ2セットの世界線を異なる時間軸を使って、測定した結果であることがこの時空図からよくわかると思います。従ってパラドックスは存在しません。 | このように、系の中で静止している棒がもう一つの系から見ると短く見えるのは、ガレージのパラドックスとして有名ですが、同じ2セットの世界線を異なる時間軸を使って、測定した結果であることがこの時空図からよくわかると思います。従ってパラドックスは存在しません。 | ||
| − | OD, OE の長さ、OA', OF の長さがわかりましたので、最後に B' | + | OD, OE の長さ、OA'の長さ(=OC'の長さ), OF の長さがわかりましたので、最後に B' の位置を求めておきましょう。 |
| − | + | B'の座標は、<math>B=\left( \begin{array} {c} 1 \\ 1 \end{array}\right)</math> をローレンツ変換するだけですので、 | |
{{eqn|Bの位置 <math>=\left( \begin{array} {c} \cosh\alpha+\sinh\alpha \\ \cosh\alpha+\sinh\alpha \end{array}\right) | {{eqn|Bの位置 <math>=\left( \begin{array} {c} \cosh\alpha+\sinh\alpha \\ \cosh\alpha+\sinh\alpha \end{array}\right) | ||
| − | =\left( \begin{array} {c} e^\alpha \\ e^\alpha \end{array}\right)</math>|21}} | + | =\left( \begin{array} {c} e^\alpha \\ e^\alpha \end{array}\right) |
| − | + | =\left( \begin{array} {c} \sqrt{\frac{1+V}{1-V}} \\ \sqrt{\frac{1+V}{1-V}} \end{array}\right) | |
| − | + | </math>|21}} | |
2016年3月7日 (月) 22:01時点における版
相対性理論のローレンツ変換は、なんかゴチャゴチャしていてめんどくさそうと感じておられる方も多いと思います。
この点に関して、実はキャンベルの「時空の幾何学」という相対性理論の解説書の中で、その美しさが詳細に述べられていたのですが、
残念ながら邦訳は何故か絶版になってしまいました。
そこで、この記事では、このローレンツ変換の秘められた美しさについて若干の説明を試みてみたいと思います。
ローレンツ変換
下図は、特殊相対性理論を説明するための図です。この図には 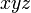 と
と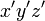 の二つの座標系が示されています。
の二つの座標系が示されています。
相対性理論ではおなじみの座標系の設定ですが、
両座標系とも慣性系で、それぞれの座標系の時刻 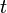 と
と 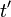 が
が 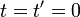 の時、2つの座標系の原点が
一致する(重なる)ものとします。
の時、2つの座標系の原点が
一致する(重なる)ものとします。
また、座標軸 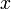 と座標軸
と座標軸 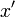 、座標軸
、座標軸 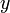 と座標軸
と座標軸 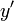 、座標軸
、座標軸 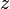 と座標軸
と座標軸 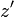 はそれぞれ同じ向きとし、
はそれぞれ同じ向きとし、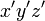 座標系は
座標系は 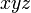 座標系の対し、
座標系の対し、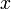 軸方向に速度
軸方向に速度 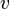 で運動しているものとします。
で運動しているものとします。
この二つの座標系では、相対性理論でおなじみのローレンツ変換の関係が成り立ちます。  は光速とすると
は光速とすると
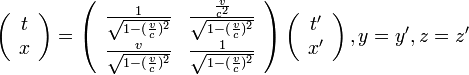
|
( 1 ) |
確かになんかごちゃごちゃしています。真ん中へんにある行列は対称行列でもないし、回転行列のような単純な美しさもありません。 いったいどこが美しいのでしょうか?
ではこれから、ローレンツ変換行列の中に隠された美しさを見てゆきましょう。
座標をちょっといじってみる
ここで、時刻を表すのに、単位が秒の 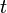 や
や 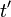 の代わりに、これらに光速をかけた、つまり単位をメートルにした値を時刻に採用します。つまり、時刻の単位を秒ではなく、メートルに変換するのです。
の代わりに、これらに光速をかけた、つまり単位をメートルにした値を時刻に採用します。つまり、時刻の単位を秒ではなく、メートルに変換するのです。
すると、ローレンツ変換は
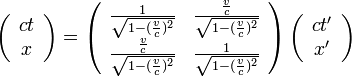
|
( 2 ) |
となります。なんと変換行列が対称行列になってしまいました。最初に比べて美しさが少し増しています。 このことは、時刻が本質的にメートルで表されるべきことを暗示していますが、先に進みましょう。
双曲線関数を使ってみる
式がより簡単になるように、速度 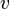 と光速
と光速  の比を
の比を 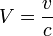 と表すことにすると、
と表すことにすると、
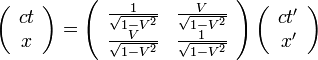
|
( 3 ) |
ここで、 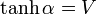 とすると、
とすると、
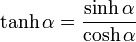
|
( 4 ) |

|
( 5 ) |
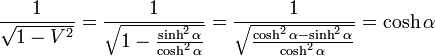
|
( 6 ) |
ですから
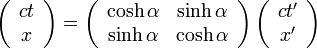
|
( 7 ) |
なんと、まるで回転行列のようなとても単純で覚えやすくて美しい行列になってしまいました。
実はこの行列は双曲回転の回転行列で、つまりローレンツ変換というのは時空座標の双曲回転なのです。
以下に双曲線回転の回転行列がどのようなものかを説明します。
そもそも双曲線関数とは
そもそも双曲線関数とは何なのでしょうか?
双曲線関数で表すことのできる座標値、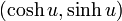 とは双曲線
とは双曲線
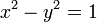
|
( 8 ) |
上の点です(但しここでは 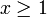 )。これは公式(5)からも明らかでしょう。それでは
)。これは公式(5)からも明らかでしょう。それでは 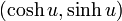 の中の
の中の 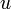 とは何なのでしょうか?
とは何なのでしょうか?
下の図を見てください。
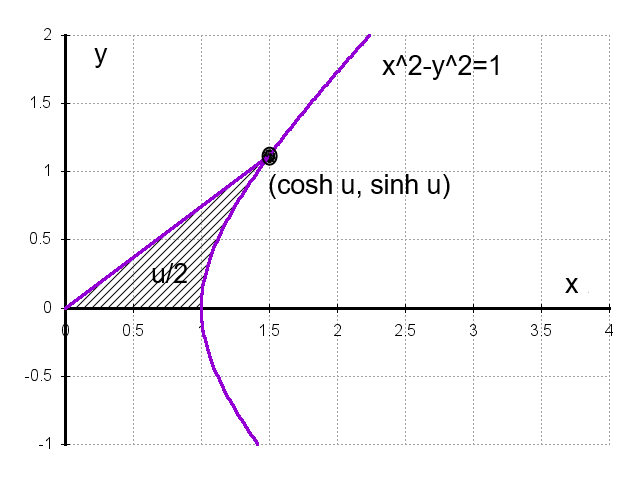
|
| 図1 双曲角 |
図の斜線の部分は双曲線と、原点と双曲線上の点 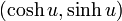 を結んだ線分と、x軸 で囲まれた領域ですが、実はこの領域の面積の2倍が u なのです。証明してみましょう。
を結んだ線分と、x軸 で囲まれた領域ですが、実はこの領域の面積の2倍が u なのです。証明してみましょう。
この領域の面積は 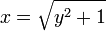 を
を  の範囲で積分して、上の三角形部分の面積を引けばよいので
の範囲で積分して、上の三角形部分の面積を引けばよいので
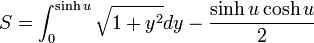
|
( 9 ) |
積分は 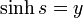 という変数変換を行うと
という変数変換を行うと
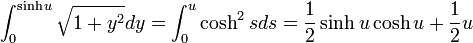
|
( 10 ) |
なので、結局
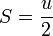
|
( 11 ) |
となります。この面積の2倍( 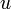 )のことを「双曲角」といいます。
)のことを「双曲角」といいます。
尚、ここまで単純に「面積」と書いてきましたが、斜線部分がX軸より下なら、双曲角はマイナスになります。
この双曲角と双曲線関数の関係は、半径1の扇形の中心角(扇形の面積の2倍)と三角関数の関係にそっくりです。
双曲回転
普通の回転は円に沿って点を動かすことですが、双曲回転は双曲線に沿って点を動かします。
下の図を見て下さい。図には双曲線 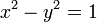 が描いて有り、
その上に双曲角が
が描いて有り、
その上に双曲角が 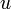 と
と  の点 A, B が描いてあります。
任意の双曲線上の点を双曲線に沿って動かす変換を双曲回転といいます。
どのような変換になるか見てみましょう。
の点 A, B が描いてあります。
任意の双曲線上の点を双曲線に沿って動かす変換を双曲回転といいます。
どのような変換になるか見てみましょう。
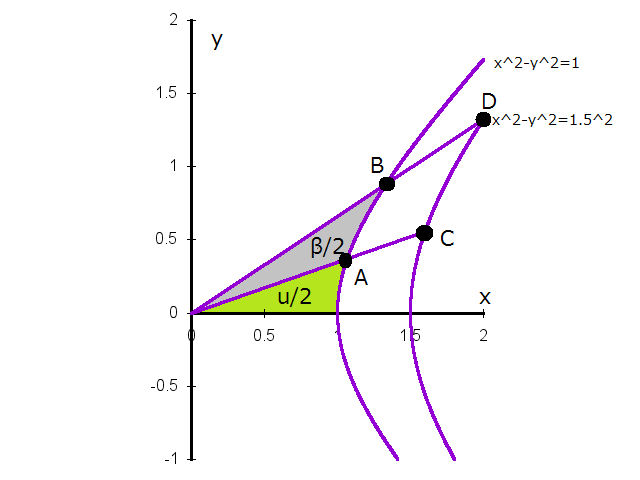
|
| 図2 双曲回転 |
点A の座標は 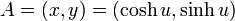 で、点B は
で、点B は 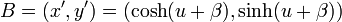 ですが、双曲線関数の角度の和の公式は
ですが、双曲線関数の角度の和の公式は
|
|
( 12 ) |
|
|
( 13 ) |
となります。これを整理し、点A(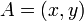 ) を 点B(
) を 点B(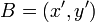 ) に変換する形にまとめると
) に変換する形にまとめると
|
|
( 14 ) |
式の中央にある行列が、既にローレンツ変換にも出てきた双曲回転の回転行列です。
この行列は、双曲線 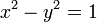 上の点だけではなく、任意の
上の点だけではなく、任意の 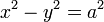 という形式の双曲線上での双曲回転にも使えます。
という形式の双曲線上での双曲回転にも使えます。
図には、双曲線 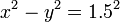 上の点Cと点Dが示してありますが、点Cと点Dへの移動は
同じ回転行列で行えます。
上の点Cと点Dが示してありますが、点Cと点Dへの移動は
同じ回転行列で行えます。
さてここまでは、双曲線 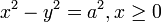 で話をしてきましたが、双曲回転は座標上の任意の点を回転可能です。しかし、双曲線
で話をしてきましたが、双曲回転は座標上の任意の点を回転可能です。しかし、双曲線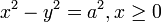 で表せる座標上の点は、全座標平面の4分の一の領域でしかありません。
で表せる座標上の点は、全座標平面の4分の一の領域でしかありません。
座標平面の全ての点をカバーするには、2種類の双曲線群 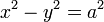 、
、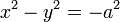 が必要です。
この双方の双曲線で双曲回転は双曲線に沿って点を動かします。
が必要です。
この双方の双曲線で双曲回転は双曲線に沿って点を動かします。
2種類の双曲線で、正の双曲回転が点をどのように動かすかを下図に示します。
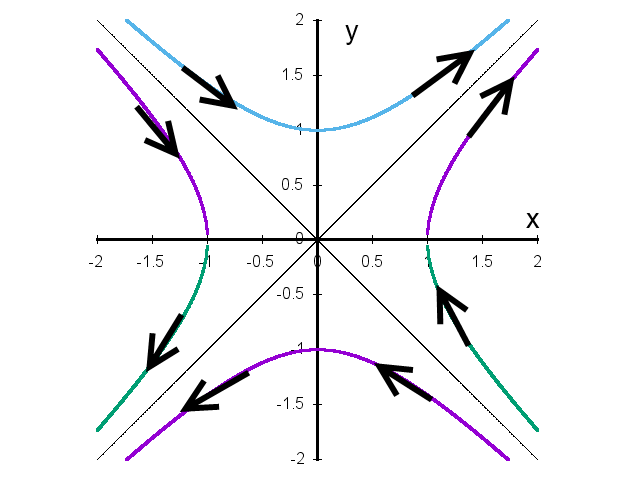
|
| 図3 全ての象限での双曲回転 |
正の双曲線回転は、図形を右斜め方向に引き伸ばし、図形を左斜め方向に圧縮することがわかると思います。
円の回転のように図形を合同に移動するのではなく、双曲回転は図形の圧縮と伸長を伴います。
つまり、時空の圧縮と伸長を伴う変換がローレンツ変換なのです。
ー次変換としてのローレンツ変換
さて、ここまでは、ローレンツ変換の美しさを 双曲回転という観点から眺めてきましたが、 ここからは 2×2の行列で行なう単純な一次変換 という観点から眺めて見ましょう。
尚、ここからは 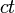 を
を 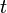 ,
, 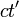 を
を 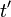 と表すことにしてしまいます。つまり
と表すことにしてしまいます。つまり 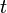 と
と 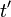 は 単位を m にした時刻を表すこととします。このような座標系を 幾何座標といいます。
は 単位を m にした時刻を表すこととします。このような座標系を 幾何座標といいます。
既に紹介してましたように、幾何座標を用いると相対性理論の式は単純化され美しくなります。 相対性理論では幾何座標を使うのが普通です。
以下の図はローレンツ変換前(双曲変換前、水色)の図形とローレンツ変換後(双曲返還後、黒)の図形を 示してあります。2個の座標系の相対速度は光速の20%です。見事に歪んでいることがわかるでしょう。
この図は見方を変えれば  時空から見た
時空から見た  時空の姿です。但し y軸,z軸は省略してあります。
時空の姿です。但し y軸,z軸は省略してあります。
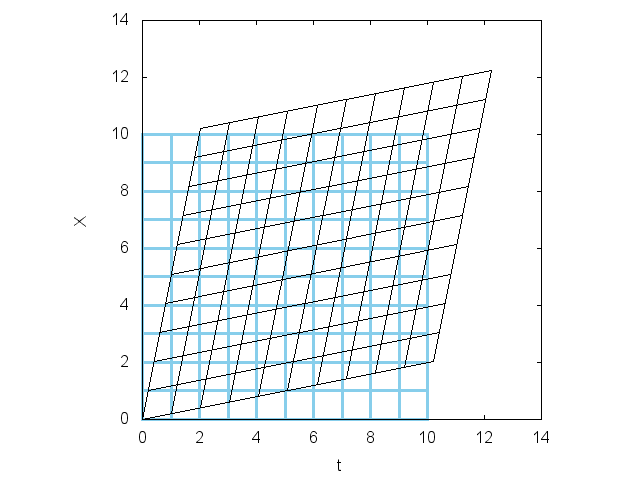
|
図4 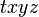 時空から見た 時空から見た 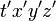 時空の姿 時空の姿
|
一次変換の性質を語るのに有効な武器は言うまでもなく行列式、固有値と固有べクトルです。
早速計算してみましょう。
ローレンツ変換の行列式は  ですから、双曲変換よって図形の
形は歪むものの面積は変化しません。
ですから、双曲変換よって図形の
形は歪むものの面積は変化しません。
ローレンツ変換の固有値は、固有方程式
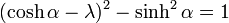
|
( 15 ) |
を解くと、
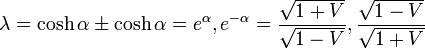
|
( 15 ) |
固有ベクトルは
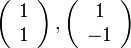
|
( 16 ) |
つまり、ローレンツ変換は 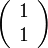 方向へ
方向へ 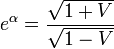 倍だけ図形を引き伸ばし、
倍だけ図形を引き伸ばし、
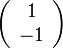 方向に
方向に 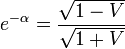 倍だけ図形を伸長する変換であることがわかります(
倍だけ図形を伸長する変換であることがわかります( 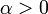 なら、つまり縮小になる )。
なら、つまり縮小になる )。
これは上の図の図形の変形の仕方からも明らかでしょう。
また、この2つの固有ベクトルの向きは「光速」を表しています。 固有ベクトルの方向は一次変換によって変化しないので、つまりこれはローレンツ変換によって 光速が光速に変換されることを示しています。
目盛りの大きさ
最後に、ローレンツ変換の座標の目盛り大きさについて考察しておきましょう。
下図は、1 m x 1 m の正方形をローレンツ変換する様子を表しています。水色の矩形が変換前、黒色が変換後です。 四角形O'A'B'Cは正方形OABCをローレンツ変換した結果です。図ではローレンツ変換の歪みをよりわかりやすくするため、系間の相対速度は光速の40%にしました。
この図は、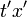 座標での時空の正方形が
座標での時空の正方形が 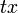 座標でどのように見えるかを示しているとも言えます。
つまり
座標でどのように見えるかを示しているとも言えます。
つまり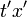 座標の時空の格子状の目盛りが、
座標の時空の格子状の目盛りが、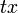 座標でどのように歪んで見えるかを示しています。
座標でどのように歪んで見えるかを示しています。
一つずつ、座標値を計算してみましょう。
まず、点A'と 点C' は、今までの議論から
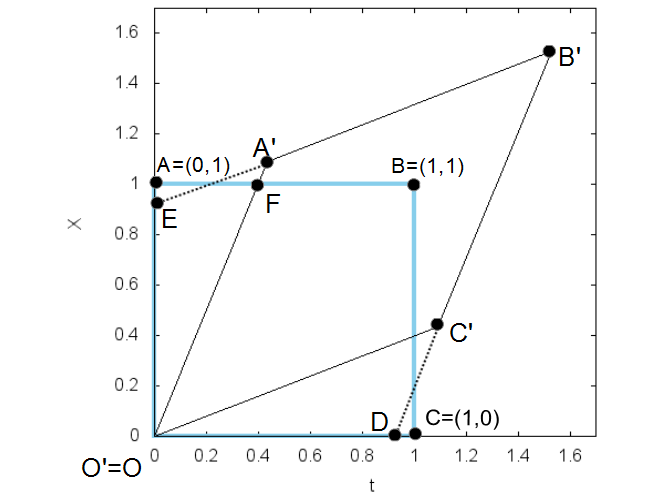
|
| 図5 ローレンツ変換の目盛り |
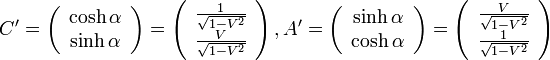
|
( 16 ) |
点C' は 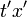 座標系では
座標系では 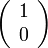 ですから、
点 O' から C' までの経路は、
ですから、
点 O' から C' までの経路は、 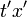 座標系では静止している物体の世界線です。
座標系では静止している物体の世界線です。
C'が線分BCより右になることから、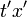 座標系で静止している物体に取り付けられている時計は、
座標系で静止している物体に取り付けられている時計は、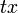 座標系から見ると遅く見えることがわかります。これが有名な「運動する物体の時間は遅くなる」ということの正体です。
座標系から見ると遅く見えることがわかります。これが有名な「運動する物体の時間は遅くなる」ということの正体です。
逆を考えてみましょう。OCは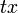 座標系で静止している物体の世界線です。この線と 点C'から O'A'に平行に引いた直線と交わる点 D は
座標系で静止している物体の世界線です。この線と 点C'から O'A'に平行に引いた直線と交わる点 D は 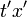 座標系では時刻が
座標系では時刻が 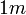 になります。
になります。
点Dの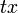 座標での
座標での 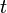 の値は、
の値は、
ODの長さ 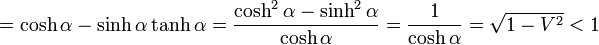
|
( 17 ) |
つまり、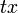 座標系で静止している物体の時計は、やはり
座標系で静止している物体の時計は、やはり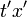 座標系から見ると遅く見えるのです。
座標系から見ると遅く見えるのです。
よくこの、互いに相手の時計が遅くなることが矛盾であるという議論を見かけますが、実際には、異なる世界線を測定した結果であり、矛盾はないことがこの時空図からよくわかると思います。
そもそもローレンツ変換は単純な一次変換であり、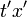 座標系の座標点と
座標系の座標点と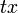 座標系の座標点との間には1対1の対応があるため、矛盾が発生しようがないのです。
座標系の座標点との間には1対1の対応があるため、矛盾が発生しようがないのです。
EA'B' とOC' は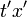 座標系で静止している、向きがX軸方向の棒の両端の世界線と考えることができます。
座標系で静止している、向きがX軸方向の棒の両端の世界線と考えることができます。
この棒の長さは 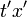 座標系では勿論
座標系では勿論 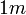 ですが、
ですが、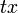 座標系では OE の長さになります。OEの長さはODの長さと同じで式(17)になり、
座標系では OE の長さになります。OEの長さはODの長さと同じで式(17)になり、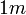 より短くなります。これが動いている物体が収縮するフィッツジェラルド収縮、或いはローレンツ収縮の正体です。
より短くなります。これが動いている物体が収縮するフィッツジェラルド収縮、或いはローレンツ収縮の正体です。
一方 OC と AB は、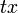 座標系で静止している、向きがX軸方向の棒の両端の世界線と考えることができます。
座標系で静止している、向きがX軸方向の棒の両端の世界線と考えることができます。
この棒は 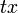 座標系では長さはもちろん
座標系では長さはもちろん 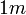 ですが、
ですが、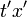 座標系では
座標系では
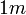 より短くなるのは OF が OA'より短いことから明らかです。
より短くなるのは OF が OA'より短いことから明らかです。
OA'の 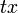 座標系での長さは
座標系での長さは
OA'の長さ 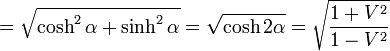
|
( 18 ) |
OFの 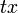 座標系での長さは
座標系での長さは
OFの長さ 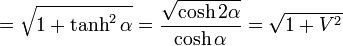
|
( 19 ) |
従って OF の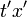 座標系での長さは
座標系での長さは
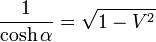
|
( 20 ) |
つまり、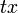 座標系で静止している棒は
座標系で静止している棒は 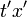 座標系からは短くみえるわけで、やはり運動している棒は短くなります。
座標系からは短くみえるわけで、やはり運動している棒は短くなります。
このように、系の中で静止している棒がもう一つの系から見ると短く見えるのは、ガレージのパラドックスとして有名ですが、同じ2セットの世界線を異なる時間軸を使って、測定した結果であることがこの時空図からよくわかると思います。従ってパラドックスは存在しません。
OD, OE の長さ、OA'の長さ(=OC'の長さ), OF の長さがわかりましたので、最後に B' の位置を求めておきましょう。
B'の座標は、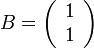 をローレンツ変換するだけですので、
をローレンツ変換するだけですので、
Bの位置 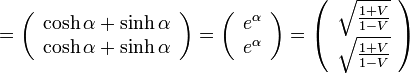
|
( 21 ) |