「指定方向のローレンツ変換」の版間の差分
提供: tknotebook
(→2次元時空のローレンツ変換) |
(→2次元時空のローレンツ変換) |
||
| 42行: | 42行: | ||
</math>|1}} | </math>|1}} | ||
| − | + | となります。これを4次元時空に拡張してみましょう。 | |
| − | + | ||
| + | 時刻の同時性のずれは、 <math>v</math>方向の位置成分に比例するので、 | ||
<math>{\boldsymbol r'}=\left( \begin{array} {c} x' \\ y' \\ z' \end{array}\right) </math> | <math>{\boldsymbol r'}=\left( \begin{array} {c} x' \\ y' \\ z' \end{array}\right) </math> | ||
、<math>{\boldsymbol u}=\left( | 、<math>{\boldsymbol u}=\left( | ||
| 58行: | 58行: | ||
位置は <math>{\boldsymbol v}</math> 方向のみローレンツ短縮が起きるので | 位置は <math>{\boldsymbol v}</math> 方向のみローレンツ短縮が起きるので | ||
| + | 位置の <math>v</math> 方向成分が <math>({\boldsymbol r'}\cdot{\boldsymbol u}){\boldsymbol u}</math>、位置の <math>v</math> に対して垂直な成分が <math>{\boldsymbol r'}-({\boldsymbol r'}\cdot{\boldsymbol u}){\boldsymbol u}</math> であることを考慮すると | ||
{{eqn|<math> | {{eqn|<math> | ||
| 65行: | 66行: | ||
</math>|3}} | </math>|3}} | ||
| + | |||
| + | これを行列に直すと、<math>\lambda = \cosh\alpha-1</math> とすれば | ||
| + | |||
| + | {{eqn|<math> | ||
| + | \left( \begin{array} {c} t \\ x \\ y \\ z \end{array}\right) = | ||
| + | |||
| + | \left( \begin{array} {cccc} | ||
| + | |||
| + | \cosh\alpha & \sinh\alpha u_x & \sinh\alpha u_y & \sinh\alpha u_z \\ | ||
| + | |||
| + | \sinh\alpha u_x & \lambda u_x^2+1 & \lambda u_xu_y & \lambda u_xu_z \\ | ||
| + | |||
| + | \sinh\alpha u_y & \lambda u_yu_x & \lambda u_y^2+1 & \lambda u_yu_z \\ | ||
| + | |||
| + | \sinh\alpha u_z & \lambda u_zu_x & \lambda u_zu_y & \lambda u_z^2+1 | ||
| + | |||
| + | \end{array}\right) | ||
| + | |||
| + | \left( \begin{array} {c} t' \\ x' \\ y' \\ z' \end{array}\right) | ||
| + | </math>|4}} | ||
2016年3月17日 (木) 11:35時点における版
ローレンツ変換は、空間1次元、時間1次元の2次元時空で扱うことが多いですが、
空間3次元、時間一次元の4次元時空ではどうなるかを探って見ました。
準備
まず座標系ですが、 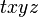 座標系と
座標系と 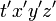 座標系の2個を用意します。
座標系の2個を用意します。
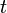 と
と 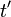 が時間軸、
が時間軸、 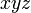 と
と 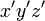 が
空間軸です。
が
空間軸です。
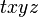 と
と 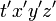 は原点一致しませんが、各軸の向きは同じとします。
また、
は原点一致しませんが、各軸の向きは同じとします。
また、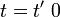 の時、
の時、 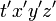 と
と 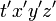 の原点が
重なるとします。
の原点が
重なるとします。
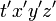 の原点の
の原点の 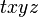 座標系での速度を
座標系での速度を
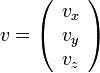 とします。
とします。
なお、座標系の単位は幾何学座標系を採用します(時間の単位は m, 速度の単位は無次元量で光速との比)。
2次元時空のローレンツ変換
美しいローレンツ変換 で紹介したローレンツ変換は
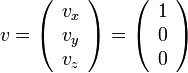 のケースで、
4次元でちゃんと書くと
のケースで、
4次元でちゃんと書くと
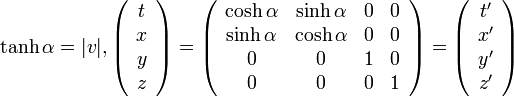
|
( 1 ) |
となります。これを4次元時空に拡張してみましょう。
時刻の同時性のずれは、 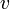 方向の位置成分に比例するので、
方向の位置成分に比例するので、
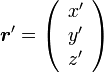 、
、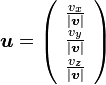 とすると
とすると
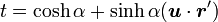
|
( 2 ) |
位置は  方向のみローレンツ短縮が起きるので
位置の
方向のみローレンツ短縮が起きるので
位置の 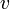 方向成分が
方向成分が 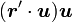 、位置の
、位置の 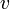 に対して垂直な成分が
に対して垂直な成分が 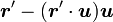 であることを考慮すると
であることを考慮すると
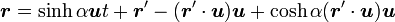
|
( 3 ) |
これを行列に直すと、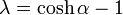 とすれば
とすれば
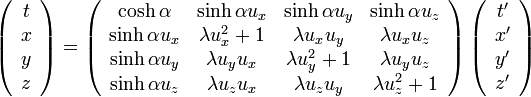
|
( 4 ) |