「複素数の表し方」の版間の差分
(→虚数を使って複素数の乗算と除算を導く) |
(→複素数のもう一つの表し方) |
||
| 85行: | 85行: | ||
と同じものを表しています。覚えておきましょう。 | と同じものを表しています。覚えておきましょう。 | ||
| + | |||
| + | ちなみに、言うまでもないことですが、<math>r</math> は <math>a + bi</math> の複素平面の原点からの距離のなので | ||
| + | ピタゴラスの定理から | ||
| + | |||
| + | {{eqnnn| <math> r = \sqrt{a^2 + b^2} </math>}} | ||
| + | |||
| + | です。 | ||
2017年8月10日 (木) 14:16時点における版
正しい複素数の表記法
ここまで、複素数を2次元ベクトルだと強調したかったので、ベクトル表現で解説を進めてきましたが そろそろ正しい表現に切り替えましょう。
正しい表現といっても、巷の複素数の表し方には大きく2種類、細かくは3種類あります。
1. 数学や物理で最も広く使われているあらわしかた
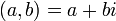
|
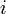 は悪名高き虚数で、b がベクトルの2番目の値であることを表しています。
は悪名高き虚数で、b がベクトルの2番目の値であることを表しています。
2. 数学や物理で最も広く使われているあらわしかたのちょっと変形
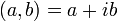
|
虚数 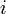 が
が 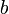 の前に来ただけですが、たまに見かけます。
の前に来ただけですが、たまに見かけます。
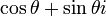
|
のように 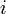 を後置すると具合が悪いケースではこちらの形式
を後置すると具合が悪いケースではこちらの形式
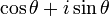
|
とすることが多いようです。
3. 電気工学ではこれ
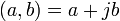
|
電気工学では小文字の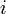 が電流を意味するのでこうなったようです。
が電流を意味するのでこうなったようです。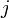 は必ず前置します。
は必ず前置します。
ここでは 1、又は2の表し方を採用します。
虚数を使って複素数の乗算と除算を導く
この書き方を採用すると、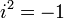 であることを
利用すると、複素数の掛算と割算の定義式を覚えなくてよくなります。何故かというと
であることを
利用すると、複素数の掛算と割算の定義式を覚えなくてよくなります。何故かというと
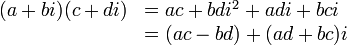
|
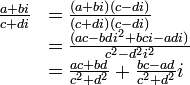
|
と今まで紹介してきた諸法則と 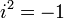 を使えば機械的に導けるからです。
を使えば機械的に導けるからです。
ほら、やっぱり怪しげな計算を使っているじゃないかと言われるかもしれませんが、 元は怪しげなものの、これは定義式だと考えて出自は無視しましょう。複素数の乗算と除算には魔法のような 不思議な能力があるので、そんなことはどうでもよいのです(^^;
複素数のもう一つの表し方
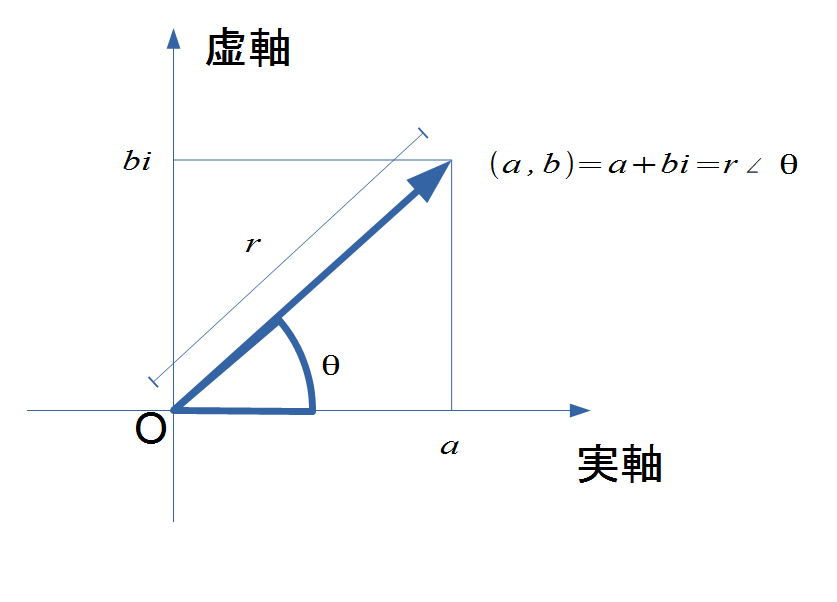
もうひとつ複素数の表記方法を紹介しましょう。大きさと角度を使う方法です。
いうまでもなく、2次元ベクトルは大きさと方向を持ちます。複素数は、上図のように複素平面での2次元の座標として 表すことができます。
その原点からの距離  と実軸となす角度
と実軸となす角度 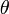 を使って複素数を
を使って複素数を
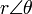
|
と表すことができます。これは
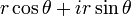
|
と同じものを表しています。覚えておきましょう。
ちなみに、言うまでもないことですが、 は
は 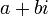 の複素平面の原点からの距離のなので
ピタゴラスの定理から
の複素平面の原点からの距離のなので
ピタゴラスの定理から
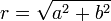
|
です。