「複素数のまとめ」の版間の差分
提供: tknotebook
(→複素数とはどういう数なのか) |
|||
| 5行: | 5行: | ||
最後に、結局複素数は何なのかをまとめておきましょう。 | 最後に、結局複素数は何なのかをまとめておきましょう。 | ||
| − | == | + | ==結局「複素数」とはどういう数なのか== |
最初の'''「[[複素数とは?]]」'''や「[[複素数の四則演算の性質]]」 では、複素数は2次元ベクトルで実数の自然な拡張であり、実数は複素数の特別な場合で、 | 最初の'''「[[複素数とは?]]」'''や「[[複素数の四則演算の性質]]」 では、複素数は2次元ベクトルで実数の自然な拡張であり、実数は複素数の特別な場合で、 | ||
| 11行: | 11行: | ||
では複素数が持つ、実数の拡張とはなんでしょうか? | では複素数が持つ、実数の拡張とはなんでしょうか? | ||
| + | |||
| + | それは「方向」(角度) です。 | ||
| + | |||
| + | では、実数には方向(角度)はないのかかというと、実は有ります。それは'''「符号」'''です。実数にはたった2種類の方向、正と負しかないのです。 | ||
| + | 実数の <math>+1</math> と <math>-1</math> を複素数の大きさと角度で表す記法で書くと | ||
| + | |||
| + | {eqnnn|<math> +1 = 1\angle 0^\circ</math>}} | ||
2017年8月11日 (金) 11:31時点における版
最後に、結局複素数は何なのかをまとめておきましょう。
結局「複素数」とはどういう数なのか
最初の「複素数とは?」や「複素数の四則演算の性質」 では、複素数は2次元ベクトルで実数の自然な拡張であり、実数は複素数の特別な場合で、 実数の性質を全て受け継いでいることをお話ししました。
では複素数が持つ、実数の拡張とはなんでしょうか?
それは「方向」(角度) です。
では、実数には方向(角度)はないのかかというと、実は有ります。それは「符号」です。実数にはたった2種類の方向、正と負しかないのです。
実数の 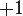 と
と 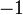 を複素数の大きさと角度で表す記法で書くと
を複素数の大きさと角度で表す記法で書くと
{eqnnn|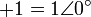 }}
}}