複素数のまとめ

最後に、結局複素数は何なのかをまとめておきましょう。

結局「複素数」とはどういう数なのか

最初の「複素数とは？」や「複素数の四則演算の性質」　では、複素数は2次元ベクトルで実数の自然な拡張であり、実数は複素数の特別な場合で、実数の性質を全て受け継いでいることをお話ししました。

では複素数が持つ、実数の拡張とはなんでしょうか？

それは「方向」(角度)　です。

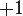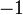では、実数には方向(角度)はないのかかというと、実は有ります。それは「符号」です。実数にはたった2種類の方向、正と負しかないのです。実数の $+1$ と $-1$ を複素数の大きさと角度で表す記法で書くと

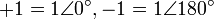
+1 = 1\angle 0^\circ, -1 =1\angle 180^\circ

となります。つまり、実数とは複素数のうち、実軸との角度が 0度、または180度の　特別な数と考えることができます。

つまり、複素数は、実数とは異なり、実軸との角度が0度や180度以外にもなれる数のことなのです。これが複素数の拡張された部分と言えるでしょう。

「複素数の乗算と除算の魔法」で、複素数の乗算や除算では複素数の実軸との角度が変わることを示しました。複素数では乗算は角度の足し算であり、除算は角度の引き算なのです。

この機能は実数にはないのでしょうか？　もちろんあります。やっぱりそれは符号です。

実数の 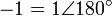$-1 = 1\angle 180^\circ$ を掛けることは、実数では符号の反転を意味しましたが、複素数では数の角度に180度を加えることを意味します。この2つは全く同等の機能です。 複素数ではこの機能を拡張し、数を掛けることで任意の角度を数に加えることができるのです。

2次元ベクトルの回転は回転行列を使えば可能ですが、2次元ベクトルだけではできません。一方複素数はそれ自体 2次元ベクトルであり、大きさと方向(角度)を持つ一方で、乗算や除算によりベクトルを回転させる機能があります。

この2次元ベクトルの回転を簡単に記述できる機能は、物理（特に光学や量子力学）や電気工学(交流理論)を記述するのに大変役に立つため、これらの学問では複素数がこれでもかというくらい多用されています。

以上長々とお付き合いありがとうございました。多分この続きは物理の部屋に書くことになると思います。