条件付停留値問題
条件付き停留値問題への応用
ここまでで、ラグランジュの未定乗数法の根本は直交補空間の直交補空間だと述べてきましたが、 これの条件付停留値問題への応用を示しましょう。
ベクトル 構文解析に失敗 (構文エラー): {{\bf {x}}}=\left({\begin{array}{c}x_{1}\\x_{2}\\\vdots \\x_{n}\end{array}}\right)
の関数 構文解析に失敗 (構文エラー): f({{\bf {x}}})
が停留値を持つのは
構文解析に失敗 (不明な関数「\label」): \mathrm{grad}f({\bf x}) = 0 \label{eq1}
の時ですが、
ベクトル 構文解析に失敗 (構文エラー): {{\bf {x}}}=\left({\begin{array}{c}x_{1}\\x_{2}\\\vdots \\x_{n}\end{array}}\right)
に対し、K個の条件(拘束条件)
構文解析に失敗 (字句解析エラー): G_l({\bf x}) = 0 (l=1~K)\label{eq2}
がある場合、関数 構文解析に失敗 (構文エラー): f({{\bf {x}}})
が停留値を取る条件は変わってきます。これを考えてみましょう。
構文解析に失敗 (構文エラー): {{\bf {x}}}
の微小変化量を 構文解析に失敗 (構文エラー): \delta {{\bf {x}}}=\left({\begin{array}{c}\delta x_{1}\\\delta x_{2}\\\vdots \\\delta x_{n}\end{array}}\right)
とすると、
構文解析に失敗 (不明な関数「\label」): \mathrm{grad}G_l({\bf x}) = \left(\begin{array}{c} \frac{\partial G_l({\bf x})}{\partial x_1} \\ \frac{\partial G_l({\bf x})}{\partial x_2} \\ \vdots \\ \frac{\partial G_l({\bf x})}{\partial x_n} \\ \end{array}\right) \label{eq3}
構文解析に失敗 (字句解析エラー): \delta G_l({\bf x}) = \mathrm{grad}G_l({\bf x})\cdot\delta{\bf x} = 0 (l=1~K) \label{eq4}
が成り立つようにしか 構文解析に失敗 (構文エラー): {{\bf {x}}}
は変化できません。
関数 構文解析に失敗 (構文エラー): f({{\bf {x}}})
が停留値を持つということは、構文解析に失敗 (構文エラー): {{\bf {x}}}
の微小変化量 構文解析に失敗 (構文エラー): \delta {{\bf {x}}}=\left({\begin{array}{c}\delta x_{1}\\\delta x_{2}\\\vdots \\\delta x_{n}\end{array}}\right)
に対し 構文解析に失敗 (構文エラー): f({{\bf {x}}})
が変化しないということなので
構文解析に失敗 (不明な関数「\label」): \mathrm{grad}f({\bf x}) = \left(\begin{array}{c} \frac{\partial f({\bf x})}{\partial x_1} \\ \frac{\partial f({\bf x})}{\partial x_2} \\ \vdots \\ \frac{\partial f({\bf x})}{\partial x_n} \\ \end{array}\right) \label{eq5}
構文解析に失敗 (不明な関数「\label」): \delta f({\bf x}) = \mathrm{grad}f({\bf x})\cdot\delta{\bf x} = 0 \label{eq6}
ラグランジュ未定乗数法の基本部分 で示しましたように、構文解析に失敗 (構文エラー): {\mathrm {grad}}f({{\bf {x}}})
は 構文解析に失敗 (構文エラー): \delta {{\bf {x}}}
が所属する部分空間の直交補空間に属します。従って、適当な係数 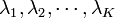 を使って
を使って
構文解析に失敗 (不明な関数「\label」): \mathrm{grad}f({\bf x}) = -\lambda_1\mathrm{grad}G_1({\bf x}) - \lambda_2\mathrm{grad}G_2({\bf x})\cdots -\lambda_K\mathrm{grad}G_K({\bf x}) \label{eq7}
とかけます。この式の意味は停留値を取るような 構文解析に失敗 (構文エラー): {{\bf {x}}}
はこの式を満たすということであり、構文解析に失敗 (構文エラー): {\mathrm {grad}}f({{\bf {x}}})
が
構文解析に失敗 (構文エラー): -\lambda _{1}{\mathrm {grad}}G_{1}({{\bf {x}}})-\lambda _{2}{\mathrm {grad}}G_{2}({{\bf {x}}})\cdots -\lambda _{K}{\mathrm {grad}}G_{K}({{\bf {x}}})
であらわされる部分空間全体になるわけではありません。
構文解析に失敗 (不明な関数「\label」): g({\bf x}) = f({\bf x}) + \lambda_1 G_1({\bf x}) + \lambda_2 G_2({\bf x})\cdots +\lambda_K G_K({\bf x}) \label{eq8}
とすると、
構文解析に失敗 (不明な関数「\label」): \mathrm{grad}g({\bf x}) = 0\label{eq9}
つまり \ref{eq2} と \ref{eq9} が停留値の条件となります。式 \ref{eq2} と \ref{eq9} は 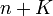 個の方程式を含みますから、
全ての未知数を求められますので、これで十分です。実際、ラグランジュの未定乗数法というのは 式 \ref{eq2} と \ref{eq9} から停留点を求めるのが普通ですが、ここでもうひとひねりしてみましょう。
個の方程式を含みますから、
全ての未知数を求められますので、これで十分です。実際、ラグランジュの未定乗数法というのは 式 \ref{eq2} と \ref{eq9} から停留点を求めるのが普通ですが、ここでもうひとひねりしてみましょう。
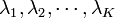 を関数の独立変数とすれば
を関数の独立変数とすれば
構文解析に失敗 (不明な関数「\label」): h({\bf x}, \lambda_1, \lambda_2, \cdots , \lambda_K) = f({\bf x}) + \lambda_1 G_1({\bf x}) + \lambda_2 G_2({\bf x})\cdots +\lambda_K G_K({\bf x}) \label{eq10}
と書けます。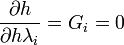 は拘束条件そのものなので、
は拘束条件そのものなので、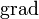 を
を 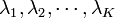 にまで拡張すれば
にまで拡張すれば
構文解析に失敗 (不明な関数「\label」): \mathrm{grad}h({\bf x}, \lambda_1, \lambda_2, \cdots , \lambda_K) = 0\label{eq11}
が 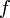 が停留値を持つ条件です。拘束条件は \ref{eq11} に取り込まれてしまった上、式 \ref{eq11} は独立変数を
が停留値を持つ条件です。拘束条件は \ref{eq11} に取り込まれてしまった上、式 \ref{eq11} は独立変数を 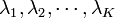 にまで拡大した停留点を求める方程式になっています。
にまで拡大した停留点を求める方程式になっています。
つまり、ラグランジュの未定乗数法は、束縛条件付き停留値問題を束縛条件なしの停留値問題に巧妙に変換するのです。
まとめ
条件付き停留値問題を、条件なし停留値問題に変換する手順は以下の通りです。
1. 元の関数 構文解析に失敗 (構文エラー): f({{\bf {x}}})
と束縛条件 構文解析に失敗 (構文エラー): G_{1}({{\bf {x}}})=0,G_{2}({{\bf {x}}})=0,\cdots ,G_{K}({{\bf {x}}})=0
から式
構文解析に失敗 (構文エラー): h({{\bf {x}}},\lambda _{1},\lambda _{2},\cdots ,\lambda _{K})=f({{\bf {x}}})+\lambda _{1}G_{1}({{\bf {x}}})+\lambda _{2}G_{2}({{\bf {x}}})+\cdots +\lambda _{K}G_{K}({{\bf {x}}})
- を作ります。
2. 以下の式より、停留値での 構文解析に失敗 (構文エラー): {{\bf {x}}}
を求めます。