ヤングの実験の光路長差について
はじめに
最近、物理系のサイトを見回っていた時、様々なサイトでヤングの実験の光路長差の計算の証明に共通する少し危うい部分を見つけました。 おそらく、最初に書いた人が書いたものをあまり吟味せずにそのまま使っているだけだと思いますが、その内容と修正案を紹介します。
ヤングの実験の光路長
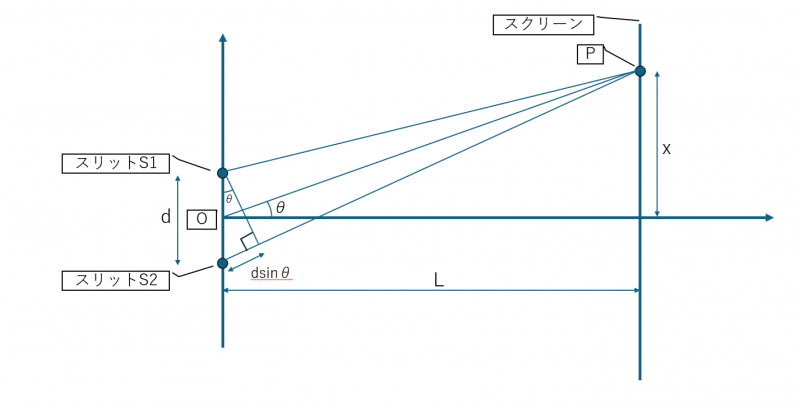
上にヤングの実験の簡単な図を示します。
ヤングの実験とは、2つのスリットに光を通すと、スリットを通過した光が相互に干渉し、スクリーン上に縞模様を映し出すという実験です。光の波動性を検証する実験といえます。
上のスリットを通った光は距離 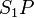 の光路長を経てスクリーン上のP点に到達。一方、下のスリットを通った光は距離
の光路長を経てスクリーン上のP点に到達。一方、下のスリットを通った光は距離 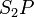 の光路長を経てスクリーン上のP点に到達。
この光路長の差が丁度波長の整数倍なら光は強め合うので、スクリーン上に明線が映し出され、この光路長の差が半波長の奇数数倍なら光は弱めあうので暗線が表示されます。
の光路長を経てスクリーン上のP点に到達。
この光路長の差が丁度波長の整数倍なら光は強め合うので、スクリーン上に明線が映し出され、この光路長の差が半波長の奇数数倍なら光は弱めあうので暗線が表示されます。
ここで問題になるのが光路長差の計算です。スリット間隔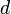 がスリットからスクリーンまでの距離
がスリットからスクリーンまでの距離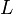 より十分に短いとき、
より十分に短いとき、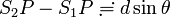 となることをどうやって求めるかです。
となることをどうやって求めるかです。
いろいろなサイトで使われている求め方
いろいろなサイトで使われている光路長差求め方はこんな感じです。
まず光路長差をピタゴラスの定理で厳密に求めます。
![\begin{align}
S_2P-S_1P &= \sqrt{L^2 + (x + \frac{d}{2})^2} - \sqrt{L^2 + (x - \frac{d}{2})^2} \\
&=L\left[\sqrt{1+\left( \frac{x+\frac{d}{2}}{L}\right)^2} - \sqrt{1+\left( \frac{x-\frac{d}{2}}{L}\right)^2} \right]
\end{align}](/mw/images/math/4/8/c/48c638e68323fbe86368d7c8ab6e77ba.png)
ここで
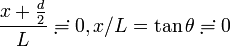
が成り立つとすると、以下の平方根のマクローリン展開で一次まで近似すれば
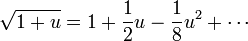
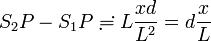
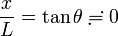 ならば
ならば 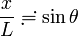 なので
なので
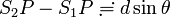
が導けます。実にシンプルですが 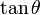 を
を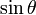 に書き換える必然性がなく、ちょっと不自然です。
に書き換える必然性がなく、ちょっと不自然です。
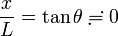 を使わない求め方
を使わない求め方
ここまで紹介した導出法では、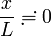 が前提になっています。つまり
が前提になっています。つまり 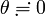 の付近でしか
の付近でしか 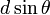 は使えません。そんなはずはないので、そこで近似の方法を少し変えてみましょう。
は使えません。そんなはずはないので、そこで近似の方法を少し変えてみましょう。
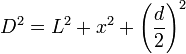 とすると
とすると
![\begin{align}
S_2P-S_1P &= \sqrt{L^2 + (x + \frac{d}{2})^2} - \sqrt{L^2 + (x - \frac{d}{2})^2} \\
&= \sqrt{L^2+x^2+\left(\frac{d}{2}\right)^2 + xd}
- \sqrt{L^2+x^2+\left(\frac{d}{2}\right)^2 - xd} \\
&=\sqrt{D^2 + xd} - \sqrt{D^2 - xd} \\
&=D\left[\sqrt{1 + \frac{d}{D}\frac{x}{D}} - \sqrt{1 - \frac{d}{D}\frac{x}{D}}\right]
\end{align}](/mw/images/math/c/7/b/c7b4bf74f4a0e53312eeb95fac13c8a8.png)
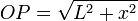
なので D は OP よりわずかに長い距離になりますから
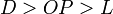
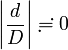 であることや
であることや 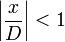 から
から
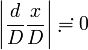
これを使って平方根のマクローリン展開で一次まで近似すれば
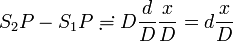
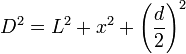
ですから、D は 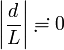 を考慮すると
を考慮すると 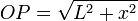 に非常に近い長さです。
に非常に近い長さです。
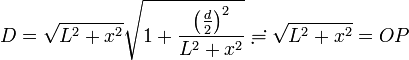
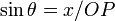 ですから、
ですから、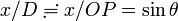
以上から
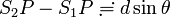
が導けます。
これは 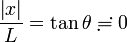 を使ってないので、
を使ってないので、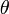 は45度でも90度でも問題なく良い近似値が求められることになります。
は45度でも90度でも問題なく良い近似値が求められることになります。
因みに 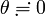 が成り立たない
が成り立たない 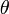 では
では
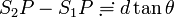
はまるで成り立たないことに注意してください。