「直交補空間」の版間の差分
提供: tknotebook
| (1人の利用者による、間の13版が非表示) | |||
| 1行: | 1行: | ||
| − | [[Category:数学]][[Category:線形代数]][[category:ラグランジュの未定乗数法]] | + | [[Category:数学]][[Category:線形代数]][[Category:数学その他]][[category:ラグランジュの未定乗数法]] |
| − | [[メインページ]]>[[数学の部屋 | + | [[メインページ]]>[[数学の部屋#ラグランジュの未定乗数法]] |
==直交補空間の定義== | ==直交補空間の定義== | ||
ラグランジュの未定乗数法の詳細な説明に入る前に、その基本的な仕掛けになっている直交補空間の説明から始めましょう。 | ラグランジュの未定乗数法の詳細な説明に入る前に、その基本的な仕掛けになっている直交補空間の説明から始めましょう。 | ||
| − | 直交補空間にはもちろん数学的に厳密な定義もありますが、ここではラグランジュの未定乗数法で使いたいだけなので、ベクトル空間 | + | 直交補空間にはもちろん数学的に厳密な定義もありますが、ここではラグランジュの未定乗数法で使いたいだけなので、ベクトル空間<math>R^n</math>と一般的な内積を使った安直な定義を |
採用することにします。 | 採用することにします。 | ||
| − | <math>{\ | + | <math>{\boldsymbol R^n}</math> べクトル空間があって、普通に内積が定義されているとします。 |
| + | |||
| + | このベクトル空間 <math>{\boldsymbol R^n}</math>の部分空間を<math>V</math>, <math>W</math> とすると、<math>V</math>に対して | ||
| + | |||
| + | |||
| + | {{eqn|<math>{\boldsymbol x} \in V \land {\boldsymbol y} \in W \to x\cdot y=0 </math>|1}} | ||
| − | |||
| − | |||
かつ | かつ | ||
| − | |||
| − | となる部分空間<math>W</math> を <math>{\ | + | |
| + | {{eqn|<math>V \bigoplus W \to {\boldsymbol R^n} </math>|2}} | ||
| + | |||
| + | |||
| + | となる部分空間<math>W</math> を <math>{\boldsymbol R^n}</math> における <math>V</math>の直交[[補空間]]といいます(<math>\bigoplus</math>は[[直和]]を表します。)。 | ||
何か難しいことを言っているように見えますが、例えば3変数(<math>x, y, z</math>)の連立方程式 | 何か難しいことを言っているように見えますが、例えば3変数(<math>x, y, z</math>)の連立方程式 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | の解<math>\left(\begin{array}{c} x\\y\\z\end{array} \right)</math>は、ベクトル <math>{\ | + | {{eqn|<math> |
| + | \begin{align}a_{11}x + a_{12}y + a_{13}z = 0 \\ | ||
| + | a_{21}x + a_{22}y + a_{23}z = 0\end{align} | ||
| + | </math>|3}} | ||
| + | |||
| + | |||
| + | の解<math>\left(\begin{array}{c} x\\y\\z\end{array} \right)</math>は、ベクトル <math>{\boldsymbol a_1} = \left(\begin{array}{c} a_{11}\\a_{12}\\a_{13}\end{array} \right)</math> と ベクトル <math>{\boldsymbol a_2} = \left(\begin{array}{c} a_{21}\\a_{22}\\a_{23}\end{array} \right)</math> を基底とする部分空間の直交補空間です。つまり、連立方程式の係数と方程式の解の関係という、中学生の頃から慣れ親しんだ関係にちょっと考察を加えた程度の概念なのです。 | ||
==直交補空間の性質== | ==直交補空間の性質== | ||
| 32行: | 39行: | ||
部分空間とその直交補空間の次元の関係は以下のようになります。 | 部分空間とその直交補空間の次元の関係は以下のようになります。 | ||
| − | <math>\dim V + \dim W = \dim R^n(= n) | + | |
| + | {{eqn|<math>\dim V + \dim W = \dim R^n(= n)</math>|4}} | ||
| + | |||
部分空間 <math>V</math> に対する直交補空間を <math>V^{\perp}</math> と表記するとした場合 | 部分空間 <math>V</math> に対する直交補空間を <math>V^{\perp}</math> と表記するとした場合 | ||
| − | <math>(V^{\perp})^{\perp} = V | + | |
| + | {{eqn|<math>(V^{\perp})^{\perp} = V</math>|5}} | ||
| + | |||
です。これはほとんど自明でしょう。直交補空間同士は対等な関係で、お互いを補いあって直和で <math>R^n</math>を形作る関係です。鋳型と鋳物の関係に似ています。元の部分空間から2回直交補空間を作ると元の部分空間に戻るのです。 | です。これはほとんど自明でしょう。直交補空間同士は対等な関係で、お互いを補いあって直和で <math>R^n</math>を形作る関係です。鋳型と鋳物の関係に似ています。元の部分空間から2回直交補空間を作ると元の部分空間に戻るのです。 | ||
2015年8月5日 (水) 05:26時点における最新版
直交補空間の定義
ラグランジュの未定乗数法の詳細な説明に入る前に、その基本的な仕掛けになっている直交補空間の説明から始めましょう。
直交補空間にはもちろん数学的に厳密な定義もありますが、ここではラグランジュの未定乗数法で使いたいだけなので、ベクトル空間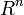 と一般的な内積を使った安直な定義を
採用することにします。
と一般的な内積を使った安直な定義を
採用することにします。
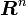 べクトル空間があって、普通に内積が定義されているとします。
べクトル空間があって、普通に内積が定義されているとします。
このベクトル空間 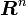 の部分空間を
の部分空間を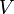 ,
, 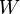 とすると、
とすると、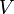 に対して
に対して
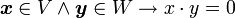
|
( 1 ) |
かつ
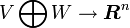
|
( 2 ) |
となる部分空間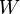 を
を 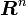 における
における 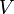 の直交補空間といいます(
の直交補空間といいます( は直和を表します。)。
は直和を表します。)。
何か難しいことを言っているように見えますが、例えば3変数(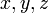 )の連立方程式
)の連立方程式
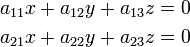
|
( 3 ) |
の解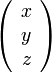 は、ベクトル
は、ベクトル 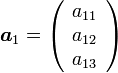 と ベクトル
と ベクトル 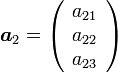 を基底とする部分空間の直交補空間です。つまり、連立方程式の係数と方程式の解の関係という、中学生の頃から慣れ親しんだ関係にちょっと考察を加えた程度の概念なのです。
を基底とする部分空間の直交補空間です。つまり、連立方程式の係数と方程式の解の関係という、中学生の頃から慣れ親しんだ関係にちょっと考察を加えた程度の概念なのです。
直交補空間の性質
部分空間とその直交補空間の次元の関係は以下のようになります。
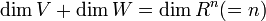
|
( 4 ) |
部分空間 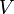 に対する直交補空間を
に対する直交補空間を 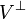 と表記するとした場合
と表記するとした場合
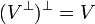
|
( 5 ) |
です。これはほとんど自明でしょう。直交補空間同士は対等な関係で、お互いを補いあって直和で 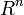 を形作る関係です。鋳型と鋳物の関係に似ています。元の部分空間から2回直交補空間を作ると元の部分空間に戻るのです。
を形作る関係です。鋳型と鋳物の関係に似ています。元の部分空間から2回直交補空間を作ると元の部分空間に戻るのです。
この性質は後でラグランジュの未定乗数法の説明で重要な意味を持ちます。
次ページ ラグランジュ未定乗数法の基本部分 へ