「複素数の四則演算の性質」の版間の差分
提供: tknotebook
(→複素数と実数の演算) |
(→加算の交換法則) |
||
| 31行: | 31行: | ||
{{eqnnn|<math> (a, b) + (c, d) = (a+c, b+d) = (c, d) + (a, b) </math>}} | {{eqnnn|<math> (a, b) + (c, d) = (a+c, b+d) = (c, d) + (a, b) </math>}} | ||
| + | |||
上記にように加算の交換法則が成り立つのは、複素数の加算の定義から明らかでしょう。 | 上記にように加算の交換法則が成り立つのは、複素数の加算の定義から明らかでしょう。 | ||
| + | |||
| + | ==乗算の交換法則== | ||
| + | |||
| + | {{eqnnn|<math> (a, b) \times (c, d) = (ac-bd, ad+bc) </math>}} | ||
| + | {{eqnnn|<math> (c, d) \times (a, b) = (ac-bd, ad+bc) </math>}} | ||
| + | |||
| + | |||
| + | 上の計算からわかるように、複素数の乗算では交換法則が成り立ちます。 | ||
| + | |||
| + | |||
| + | ==分配法則== | ||
| + | |||
| + | {{eqnnn|<math> (a, b) \times \left \{ (c, d) + (e, f) \right \} | ||
| + | = (a, b) \times (c+e, d+f) | ||
| + | =(ac+ae - bd-bf, ad+af+bc+be) </math>}} | ||
| + | |||
| + | {{eqnnn|<math> (a, b) \times (c, d) + (a, b) \times (e, f) | ||
| + | = (ac-bd, ad+bc) + (ae-bf, af+be) | ||
| + | = (ac+ae - bd-bf, ad+af+bc+be) </math>}} | ||
| + | |||
| + | |||
| + | 上の計算からわかるように、複素数の加算と乗算では分配法則が実数の場合と同様に成り立ちます。 | ||
2017年8月7日 (月) 15:27時点における版
ひとつ前の解説「複素数とは?」では、複素数の演算が実数同士の演算を変えないことを示しました。
このページではもう少し複素数の性質を探ってみましょう。
複素数と実数の演算
加減算は簡単なので、掛け算と除算を示しましょう。
1. 複素数と実数掛け算
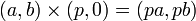
|
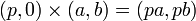
|
2. 複素数を実数で割る
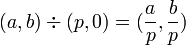
|
3. 実数を複素数で割る
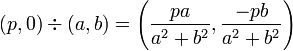
|
1, 2 は2次元ベクトルに実数をかけた場合と同じなのでわかりやすいでしょう。単純にベクトルの大きさが実数倍に変わるだけです。
実数を複素数で割ると独特の結果になりますが、これは後で解説します。
加算の交換法則
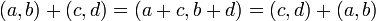
|
上記にように加算の交換法則が成り立つのは、複素数の加算の定義から明らかでしょう。
乗算の交換法則
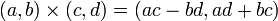
|
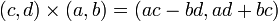
|
上の計算からわかるように、複素数の乗算では交換法則が成り立ちます。
分配法則
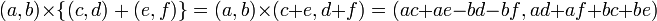
|
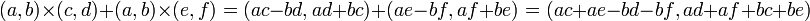
|
上の計算からわかるように、複素数の加算と乗算では分配法則が実数の場合と同様に成り立ちます。