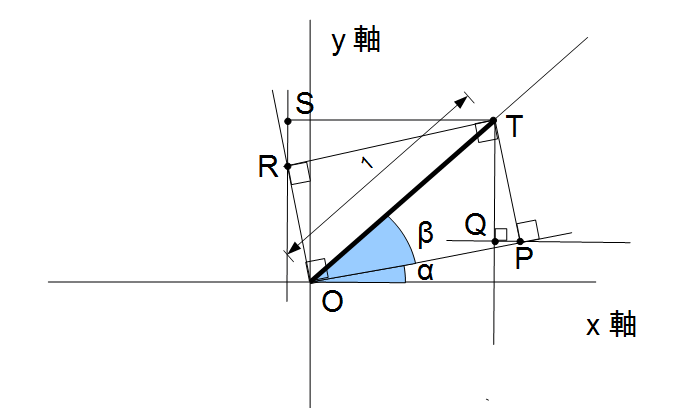
角度の加法定理

線形代数のカテゴリなのに角度の公式は少し不似合かもしれませんが、この公式は内積と深い関わり合いがあるのでこれを最初の話題にしておきます。高校になると3角関数の公式として加法定理というのを習います。こんな公式です。

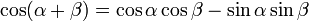
\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta

( 1 )

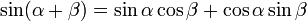
\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta

( 2 )

余弦定理などを使ってスマートに説明する方法もありますが、ここでは幾何学的な説明のみで加法定理を導いてみましょう。下の図を見てください。

図には原点が片方の端点で、長さが1で、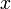 $x$ 軸とのなす角が 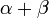$\alpha+\beta$ になる線分 OTがあります。 Tの座標は当然ながら

構文解析に失敗 (不明な関数「\tag」): x = \cos(\alpha + \beta), y = \sin(\alpha+\beta) \tag{3}

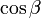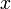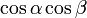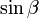です。OPの長さは $\cos \beta$ ですから、Pの $x$ 座標は $\cos\alpha\cos\beta$ 。 TPの長さは $\sin \beta$ ですから、QPの長さは 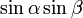$\sin\alpha\sin\beta$ 。従って, T(とQ)の 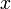$x$ 座標は　

構文解析に失敗 (不明な関数「\tag」): \cos\alpha\cos\beta - \sin\alpha\sin\beta \tag{4}

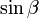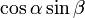ORの長さは $\sin \beta$ ですから、Rのy座標は $\cos\alpha\sin\beta$ 。

RTの長さは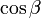 $\cos \beta$ ですから、RSの長さは 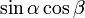$\sin\alpha\cos\beta$ 従って, T(とS)のy座標は　

構文解析に失敗 (字句解析エラー): \sin\alpha\cos\beta + \cos\alpha\sin\beta　\tag{5}

これで公式(1), (2)が正しいことが確かめられました。

もちろんこの説明は完全ではありません。αとβが鈍角になった時などで図形の形が変わるため、念のためにそういう場合でも大丈夫か検証する必要があるからです。厳密に証明したい人は、是非様々なパターンを網羅して、式の形が変わらないことを確認してみてください。

案内メニュー