「回転行列と複素数の積」の版間の差分
| 10行: | 10行: | ||
2次元座標で原点を中心にした回転は、簡単な行列で表現できます。回転行列と呼ばれます。さっそく導いてみましょう。 | 2次元座標で原点を中心にした回転は、簡単な行列で表現できます。回転行列と呼ばれます。さっそく導いてみましょう。 | ||
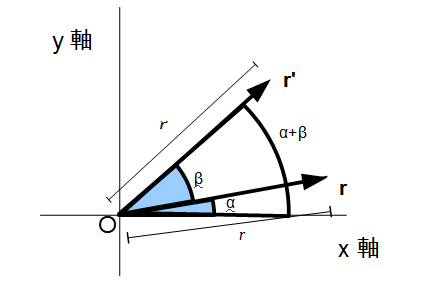
| − | 任意の点 | + | 任意の点 <math>{\bf r} = \left( \begin{array} {cc} x\\ y \end{array}\right) </math> を、原点を中心に反時計回りに <math>\beta</math> 回転させてみましょう。回転後の座標を <math>{\bf r'} = \left( \begin{array} {cc}x'\\ y' \end{array}\right)</math> とし、<math>{\bf r}</math> の極座標での長さを <math>r</math> 偏角を <math>\alpha</math> とすると |
| − | + | <math> x = r\cos\alpha \label{rx} </math> | |
| − | + | <math> y = r\sin\alpha \label{ry} </math> | |
| − | + | <math> x' = r\cos(\alpha+\beta) \label{r'x} </math> | |
| − | + | <math> y' = r\sin(\alpha+\beta) \label{r'y} </math> | |
\eqref{r'x} と \eqref{r'y} は[[角度の加法定理]]をあてはめると | \eqref{r'x} と \eqref{r'y} は[[角度の加法定理]]をあてはめると | ||
| − | + | <math> x' = r\cos\alpha\cos\beta-r\sin\alpha\sin\beta \label{r'x2} </math> | |
| − | + | <math> y' = r\sin\alpha\cos\beta+r\cos\alpha\sin\beta \label{r'y2} </math> | |
これに、\eqref{rx} と \eqref{ry} を使うと | これに、\eqref{rx} と \eqref{ry} を使うと | ||
| − | + | <math> x' = \cos\beta\cdot x-\sin\beta\cdot y \label{r'x3} </math> | |
| − | + | <math> y' = x\sin\beta\cdot x + \cos\beta\cdot y \label{r'y3} </math> | |
これを行列を使って書き直せば | これを行列を使って書き直せば | ||
| − | + | <math> \left( \begin{array} {cc}x'\\ y' \end{array}\right) = | |
\left( \begin{array} {cc} \cos\beta & -sin\beta \\ \sin\beta& \ cos\beta \end{array}\right) | \left( \begin{array} {cc} \cos\beta & -sin\beta \\ \sin\beta& \ cos\beta \end{array}\right) | ||
| − | \left( \begin{array} {cc} x\\ y \end{array}\right) \label{RotationMatrix} | + | \left( \begin{array} {cc} x\\ y \end{array}\right) \label{RotationMatrix} </math> |
| − | これが2次元の回転行列と呼ばれるもので、 | + | これが2次元の回転行列と呼ばれるもので、<math>{\bf r} = \left( \begin{array} {cc} x\\ y \end{array}\right) </math> を角度βだけ回転させ、<math>{\bf r'} = \left( \begin{array} {cc}x'\\ y' \end{array}\right)</math> に変換します。 |
この回転行列を2個掛け合わせたらどうなるのでしょうか? | この回転行列を2個掛け合わせたらどうなるのでしょうか? | ||
| − | + | <math> | |
\left( \begin{array} {cc} \cos\alpha & -\sin\alpha \\ \sin\alpha& \cos\alpha \end{array}\right) | \left( \begin{array} {cc} \cos\alpha & -\sin\alpha \\ \sin\alpha& \cos\alpha \end{array}\right) | ||
| 45行: | 45行: | ||
\label{SeqRotationMatrix} | \label{SeqRotationMatrix} | ||
| − | + | </math> | |
この行列はβの回転とαの回転を順次行うわけですから、α+βだけの回転になるはずで、これを回転行列で表現すると | この行列はβの回転とαの回転を順次行うわけですから、α+βだけの回転になるはずで、これを回転行列で表現すると | ||
| − | + | <math> | |
\left( \begin{array} {cc} \cos(\alpha+\beta) & -\sin(\alpha+\beta) \\ \sin(\alpha+\beta)& \cos(\alpha+\beta) \end{array}\right) | \left( \begin{array} {cc} \cos(\alpha+\beta) & -\sin(\alpha+\beta) \\ \sin(\alpha+\beta)& \cos(\alpha+\beta) \end{array}\right) | ||
\label{AddRotation} | \label{AddRotation} | ||
| − | + | </math> | |
となるはずです。\eqref{SeqRotationMatrix} と \eqref{AddRotation} は一致するはずですが、\eqref{SeqRotationMatrix} を計算すると | となるはずです。\eqref{SeqRotationMatrix} と \eqref{AddRotation} は一致するはずですが、\eqref{SeqRotationMatrix} を計算すると | ||
| − | + | <math> | |
\left( \begin{array} {cc} | \left( \begin{array} {cc} | ||
\cos\alpha\cos\beta-\sin\alpha\sin\beta & | \cos\alpha\cos\beta-\sin\alpha\sin\beta & | ||
| 64行: | 64行: | ||
\end{array}\right) | \end{array}\right) | ||
\label{AddRotation2} | \label{AddRotation2} | ||
| − | + | </math> | |
となり、\eqref{AddRotation}と\eqref{AddRotation2}の関係は[[角度の加法定理]]と一致しています。 | となり、\eqref{AddRotation}と\eqref{AddRotation2}の関係は[[角度の加法定理]]と一致しています。 | ||
| 72行: | 72行: | ||
==複素数の積== | ==複素数の積== | ||
| − | 複素数の掛け算の演算規則は | + | 複素数の掛け算の演算規則は <math>(a+\mathrm{i}\cdot b)(c+\mathrm{i}\cdot d)=ac-bd+\mathrm{i}\cdot (ad+bc) </math> と単純ですが、 |
にもかかわらず幾何学的には「回転」と密接に関係しています。この関係が複素数の有用さの源泉になっています。その秘密をちょっと探ってみましょう。 | にもかかわらず幾何学的には「回転」と密接に関係しています。この関係が複素数の有用さの源泉になっています。その秘密をちょっと探ってみましょう。 | ||
| − | 複素数 | + | 複素数 <math>c1</math>、<math>c2</math> をその大きさ <math>r_1</math>、 <math>r_2</math> と偏角<math>\alpha</math>、<math>\beta</math> で表すと |
| − | + | <math> c_1 = r_1\cos\alpha + \mathrm{i}\cdot r_1\sin\alpha \label{c1} </math> | |
| − | + | <math> c_2 = r_2\cos\beta + \mathrm{i}\cdot r_2\sin\beta \label{c2} </math> | |
| − | となります。ここで複素数の積 | + | となります。ここで複素数の積 <math>c_1c_2</math>を計算してみましょう。 |
| − | + | <math> c_1c_2=r_1r_2(\cos\alpha\cos\beta-\sin\alpha\sin\beta) + \mathrm{i}\cdot r_1r_2(\sin\alpha\cos\beta+\cos\alpha\sin\beta) \label{ComplexProduct}</math> | |
この式に角度の加法定理を当てはめると | この式に角度の加法定理を当てはめると | ||
| − | + | <math> c_1c_2=r_1r_2\cos(\alpha+\beta) + \mathrm{i}\cdot r_1r_2\sin(\alpha+\beta) | |
| − | = r_1r_2(\cos(\alpha+\beta) + \mathrm{i}\cdot\sin(\alpha+\beta)) \label{ComplexProduct2} | + | = r_1r_2(\cos(\alpha+\beta) + \mathrm{i}\cdot\sin(\alpha+\beta)) \label{ComplexProduct2} </math> |
以上から、複素数の掛け算とは、大きさを掛け、偏角を足す計算であることがわかります。 | 以上から、複素数の掛け算とは、大きさを掛け、偏角を足す計算であることがわかります。 | ||
2014年12月28日 (日) 11:42時点における版
初歩的な話で申し訳ありませんが、他の説明で使いたいので、ここではベクトルと複素数と2次元回転の関係の話を書き留めておきます。
回転行列
2次元座標で原点を中心にした回転は、簡単な行列で表現できます。回転行列と呼ばれます。さっそく導いてみましょう。
任意の点 構文解析に失敗 (構文エラー): {{\bf {r}}}=\left({\begin{array}{cc}x\\y\end{array}}\right)
を、原点を中心に反時計回りに回転させてみましょう。回転後の座標を 構文解析に失敗 (構文エラー): {{\bf {r'}}}=\left({\begin{array}{cc}x'\\y'\end{array}}\right) とし、構文解析に失敗 (構文エラー): {{\bf {r}}} の極座標での長さを
偏角を
とすると
構文解析に失敗 (不明な関数「\label」): x = r\cos\alpha \label{rx}
構文解析に失敗 (不明な関数「\label」): y = r\sin\alpha \label{ry}
構文解析に失敗 (不明な関数「\label」): x' = r\cos(\alpha+\beta) \label{r'x}
構文解析に失敗 (不明な関数「\label」): y' = r\sin(\alpha+\beta) \label{r'y}
\eqref{r'x} と \eqref{r'y} は角度の加法定理をあてはめると
構文解析に失敗 (不明な関数「\label」): x' = r\cos\alpha\cos\beta-r\sin\alpha\sin\beta \label{r'x2}
構文解析に失敗 (不明な関数「\label」): y' = r\sin\alpha\cos\beta+r\cos\alpha\sin\beta \label{r'y2}
これに、\eqref{rx} と \eqref{ry} を使うと
構文解析に失敗 (不明な関数「\label」): x' = \cos\beta\cdot x-\sin\beta\cdot y \label{r'x3}
構文解析に失敗 (不明な関数「\label」): y' = x\sin\beta\cdot x + \cos\beta\cdot y \label{r'y3}
これを行列を使って書き直せば
構文解析に失敗 (不明な関数「\label」): \left( \begin{array} {cc}x'\\ y' \end{array}\right) = \left( \begin{array} {cc} \cos\beta & -sin\beta \\ \sin\beta& \ cos\beta \end{array}\right) \left( \begin{array} {cc} x\\ y \end{array}\right) \label{RotationMatrix}
これが2次元の回転行列と呼ばれるもので、構文解析に失敗 (構文エラー): {{\bf {r}}}=\left({\begin{array}{cc}x\\y\end{array}}\right)
を角度βだけ回転させ、構文解析に失敗 (構文エラー): {{\bf {r'}}}=\left({\begin{array}{cc}x'\\y'\end{array}}\right)
に変換します。
この回転行列を2個掛け合わせたらどうなるのでしょうか?
構文解析に失敗 (不明な関数「\label」): \left( \begin{array} {cc} \cos\alpha & -\sin\alpha \\ \sin\alpha& \cos\alpha \end{array}\right) \left( \begin{array} {cc} \cos\beta & -\sin\beta \\ \sin\beta& \cos\beta \end{array}\right) \label{SeqRotationMatrix}
この行列はβの回転とαの回転を順次行うわけですから、α+βだけの回転になるはずで、これを回転行列で表現すると
構文解析に失敗 (不明な関数「\label」): \left( \begin{array} {cc} \cos(\alpha+\beta) & -\sin(\alpha+\beta) \\ \sin(\alpha+\beta)& \cos(\alpha+\beta) \end{array}\right) \label{AddRotation}
となるはずです。\eqref{SeqRotationMatrix} と \eqref{AddRotation} は一致するはずですが、\eqref{SeqRotationMatrix} を計算すると
構文解析に失敗 (不明な関数「\label」): \left( \begin{array} {cc} \cos\alpha\cos\beta-\sin\alpha\sin\beta & -\sin\alpha\cos\beta-\cos\alpha\sin\beta \\ \sin\alpha\cos\beta+\cos\alpha\sin\beta & \cos\alpha\cos\beta-\sin\alpha\sin\beta \end{array}\right) \label{AddRotation2}
となり、\eqref{AddRotation}と\eqref{AddRotation2}の関係は角度の加法定理と一致しています。
以上のように回転行列の積は回転角度の和に対応しており、角度の加法定理を覚えておけば回転行列は簡単に導けますし、回転行列を覚えておけば角度の加法定理を容易に導けます。
複素数の積
複素数の掛け算の演算規則は 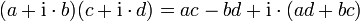 と単純ですが、
にもかかわらず幾何学的には「回転」と密接に関係しています。この関係が複素数の有用さの源泉になっています。その秘密をちょっと探ってみましょう。
と単純ですが、
にもかかわらず幾何学的には「回転」と密接に関係しています。この関係が複素数の有用さの源泉になっています。その秘密をちょっと探ってみましょう。
複素数 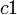 、
、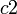 をその大きさ
をその大きさ 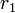 、
、 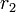 と偏角
と偏角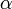 、
、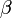 で表すと
で表すと
構文解析に失敗 (不明な関数「\label」): c_1 = r_1\cos\alpha + \mathrm{i}\cdot r_1\sin\alpha \label{c1}
構文解析に失敗 (不明な関数「\label」): c_2 = r_2\cos\beta + \mathrm{i}\cdot r_2\sin\beta \label{c2}
となります。ここで複素数の積 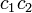 を計算してみましょう。
を計算してみましょう。
構文解析に失敗 (不明な関数「\label」): c_1c_2=r_1r_2(\cos\alpha\cos\beta-\sin\alpha\sin\beta) + \mathrm{i}\cdot r_1r_2(\sin\alpha\cos\beta+\cos\alpha\sin\beta) \label{ComplexProduct}
この式に角度の加法定理を当てはめると
構文解析に失敗 (不明な関数「\label」): c_1c_2=r_1r_2\cos(\alpha+\beta) + \mathrm{i}\cdot r_1r_2\sin(\alpha+\beta) = r_1r_2(\cos(\alpha+\beta) + \mathrm{i}\cdot\sin(\alpha+\beta)) \label{ComplexProduct2}
以上から、複素数の掛け算とは、大きさを掛け、偏角を足す計算であることがわかります。
つまり複素数の掛け算の単純な規則を覚えておけば、角度の加法定理は簡単に導けるということです。
次ページ 3次元の内積の幾何学的な性質 へ