「2次元の内積の幾何学的な性質」の版間の差分
提供: tknotebook
| 14行: | 14行: | ||
[[ファイル:2次元の内積の幾何学的性質.png]] | [[ファイル:2次元の内積の幾何学的性質.png]] | ||
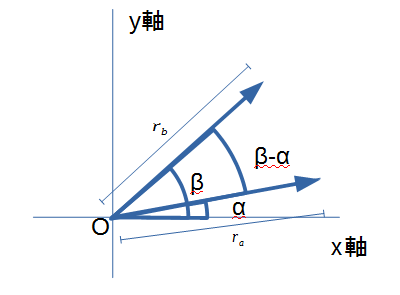
| − | ベクトル <math>\ | + | ベクトル <math>\boldsymbol a</math> と <math>\boldsymbol b</math> を図のようにベクトルの長さと偏角 <math>r_a, \alpha</math>、<math>r_b, \beta</math> で、表すと、 |
それぞれのベクトルの <math>x</math>、 <math>y</math> 成分は | それぞれのベクトルの <math>x</math>、 <math>y</math> 成分は | ||
| − | <math>{\ | + | <math>{\boldsymbol a} = (r_a\cos\alpha, r_a\sin\alpha)</math>、<math>{\boldsymbol b} = |
(r_b\cos\beta, r_b\sin\beta)</math> となります。従って内積は | (r_b\cos\beta, r_b\sin\beta)</math> となります。従って内積は | ||
<math> | <math> | ||
| − | {\ | + | {\boldsymbol a}\cdot {\boldsymbol b}= |
r_a\cos\alpha \cdot r_b\cos\beta+r_a\sin\alpha \cdot r_b\sin\beta= | r_a\cos\alpha \cdot r_b\cos\beta+r_a\sin\alpha \cdot r_b\sin\beta= | ||
r_a r_b(\cos\alpha\cos\beta+\sin\alpha\sin\beta) | r_a r_b(\cos\alpha\cos\beta+\sin\alpha\sin\beta) | ||
| 31行: | 31行: | ||
<math> | <math> | ||
| − | {\ | + | {\boldsymbol a}\cdot {\boldsymbol b} = r_a r_b\cos(\beta-\alpha) |
\tag{3} | \tag{3} | ||
</math> | </math> | ||
| − | という単純かつ美しい式に変身します。式中に現れる <math>\beta-\alpha</math> はベクトル <math>\ | + | という単純かつ美しい式に変身します。式中に現れる <math>\beta-\alpha</math> はベクトル <math>\boldsymbol a</math> と <math>\boldsymbol b</math> がなす角度です。 |
| − | つまり、内積はベクトル <math>\ | + | つまり、内積はベクトル <math>\boldsymbol a</math> と <math>\boldsymbol b</math> が同じ向きの時 <math>r_a r_b</math> となり、正のもっとも大きな値になります。 |
| − | <math>\ | + | <math>\boldsymbol a</math> と <math>\boldsymbol b</math> が垂直の時 <math>0</math> になります。 |
次ページ [[回転行列と複素数の積]] へ | 次ページ [[回転行列と複素数の積]] へ | ||
2014年12月28日 (日) 17:59時点における版
2次元の内積の定義は簡単です。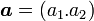 、
、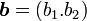 とすると内積は
とすると内積は
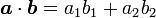
|
( 1 ) |
この単純な定義からは信じられないことですが、内積には非常に美しい幾何学的な性質があります。
ベクトル 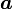 と
と 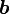 を図のようにベクトルの長さと偏角
を図のようにベクトルの長さと偏角 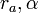 、
、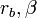 で、表すと、
それぞれのベクトルの
で、表すと、
それぞれのベクトルの 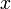 、
、 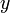 成分は
成分は
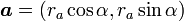 、
、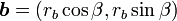 となります。従って内積は
となります。従って内積は
構文解析に失敗 (不明な関数「\tag」): {\boldsymbol a}\cdot {\boldsymbol b}= r_a\cos\alpha \cdot r_b\cos\beta+r_a\sin\alpha \cdot r_b\sin\beta= r_a r_b(\cos\alpha\cos\beta+\sin\alpha\sin\beta) \tag{2}
となります。どこかで見た形ですよね? そう、角度の加法定理です。角度の加法定理で 紹介した定理を符号を注意して当てはめると、内積は
構文解析に失敗 (字句解析エラー): {\boldsymbol a}\cdot {\boldsymbol b} = r_a r_b\cos(\beta-\alpha) \tag{3}
という単純かつ美しい式に変身します。式中に現れる 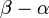 はベクトル
はベクトル 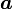 と
と 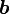 がなす角度です。
つまり、内積はベクトル
がなす角度です。
つまり、内積はベクトル 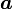 と
と 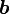 が同じ向きの時
が同じ向きの時 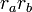 となり、正のもっとも大きな値になります。
となり、正のもっとも大きな値になります。
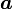 と
と 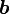 が垂直の時
が垂直の時  になります。
になります。
次ページ 回転行列と複素数の積 へ